幼女でもわかる単相PWMコンバータのベクトル制御

前回の記事で紹介した単相PWMコンバータについて，その制御系に関して少し詳しく解説します．

　

この単相PWMコンバータは電流制御方法として仮想軸電流ベクトル制御というものを使っています．
(この名称は仮想的な二軸電流に対してベクトル制御をするということで，私が勝手に命名したものです．)

ベクトル制御とは，多相交流において元々の座標系(固定座標系)上での電流ベクトルに座標変換(dq変換)を適用し，回転座標系あるいはdq座標系と呼ばれる直交座標系上のベクトルとして電流を制御することを一般的にいいます．dq座標系は，回転する基準のベクトルに対する，大きさと位相の情報を持つ2本の直流として表されます．つまり，dq座標系では，交流をあたかも直流のように扱うことができるということです．回転する基準のベクトルとは基本的に，誘導モータでは二次磁束，同期モータでは界磁磁束，そして系統連系インバータやPWMコンバータでは電源電圧が選ばれます．その位相角を用い，電流ベクトルを基準ベクトルの回転とは反対方向に回転変換することで，dq座標系における直流，すなわちd軸電流とq軸電流が取得されます．d軸電流は基準ベクトルの位相と一致した方向の成分で，モータでは回転子磁束，系統連系では有効電力に寄与します．また，q軸電流はd軸に直行する成分であり，モータではトルク，系統連系では無効電力に寄与します．すなわち，2本それぞれの電流を操作することにより，それぞれに寄与する量を独立的に制御できるということになります．

通常のベクトル制御は三相の電力変換器において適用されます．二相以上の交流でないと二次元のベクトル量として表されないので，の変換である回転変換が適用できず，dq変換ができません．すなわち，スカラー量である単相の電力変換器において，通常のベクトル制御はできないということになります．

ここでは，単相に対して演算によりもう一つの相を補うことで二相とし，単相電源でもベクトル制御が可能となるPWMコンバータ制御系の構成方法を紹介します．単相PWMコンバータにベクトル制御を適用することで，電流の追従性が向上し，また無効電力の調整が容易にできるようになります．まずは一般的なPWMコンバータのベクトル制御を考えるため，dq座標系上のプラントのモデル化と，ベクトル制御を適用するための電流制御系の構成方法を解説します．その後に，単相のPWMコンバータにベクトル制御を適用するための，二次一般化積分器ベース位相同期ループ(SOGI-based PLL)と仮想軸エミュレーション(FAE)について解説します．

記号の定義

$$\boldsymbol{e}_{\alpha\beta}=\left[\begin{array}{cc}e_\alpha & e_\beta \end{array} \right]^T$$$$\boldsymbol{v}_{\alpha\beta}=\left[\begin{array}{cc}v_\alpha & v_\beta \end{array} \right]^T$$$$\boldsymbol{i}_{\alpha\beta}=\left[\begin{array}{cc}i_\alpha & i_\beta \end{array} \right]^T$$$$\boldsymbol{e}_{dq}=\left[\begin{array}{cc}e_d & e_q \end{array} \right]^T$$$$\boldsymbol{v}_{dq}=\left[\begin{array}{cc}v_d & v_q \end{array} \right]^T$$$$\boldsymbol{i}_{dq}=\left[\begin{array}{cc}i_d & i_q \end{array} \right]^T$$$$\boldsymbol{I}=\left[\begin{array}{cc}1 & 0 \\ 0 & 1\end{array}\right]$$$$\boldsymbol{J}=\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]$$$$\boldsymbol{R}(\theta)=\left[\begin{array}{cc}\cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{array}\right]$$

PWMコンバータのdq座標モデル

二相交流を電源とするPWMコンバータを考え，その電流制御系のプラントをモデル化します．
図1に示すような，リアクトルのインダクタンスを，直列抵抗成分をとし，二相の電源電圧をとする二相PWMコンバータを考えます．

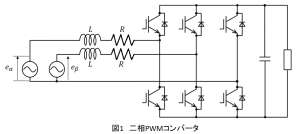
状態平均化法より，コンバータのアーム間電圧は連続的に変化する交流電圧源とみなすことができます．それをとし，図2のようになります．また相電流をとします．したがって，(1)式のような電圧方程式が成り立ちます．

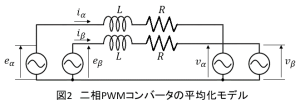
$$\boldsymbol{e}_{\alpha\beta}=L \frac{d \boldsymbol{i}_{\alpha\beta}}{dt}+ R \boldsymbol{i}_{\alpha\beta}+ \boldsymbol{v}_{\alpha\beta}\tag{1}$$

ここで，回転行列より，固定座標系におけるのdq座標系への写像を(2)式のように考えます．はdq変換により得られるdq座標系上でのベクトルです．

$$\boldsymbol{f}_{dq}=\boldsymbol{R}^T(\theta)\boldsymbol{f}_{\alpha\beta}\tag{2}$$

また，dq座標系から固定座標系への逆変換は(3)式となります．

$$\boldsymbol{f}_{\alpha\beta}=\boldsymbol{R}(\theta)\boldsymbol{f}_{dq}\tag{3}$$

，，のdq座標系への写像により得られるベクトルをそれぞれ，，とし，(1)式の電圧方程式に対しdq変換を適用します．(3)式より(1)式の各ベクトルを置き換えると(4)式となります．

$$\boldsymbol{R}(\theta)\boldsymbol{e}_{dq}=L \frac{d}{dt}\{\boldsymbol{R}(\theta)\boldsymbol{i}_{dq}\}+ R \boldsymbol{R}(\theta)\boldsymbol{i}_{dq}+\boldsymbol{R}(\theta) \boldsymbol{v}_{dq}\tag{4}$$

両辺に左からを掛けると(5)式となります．

$$\boldsymbol{e}_{dq}=L \boldsymbol{R}^T(\theta)\frac{d}{dt}\{\boldsymbol{R}(\theta)\boldsymbol{i}_{dq}\}+ R\boldsymbol{i}_{dq}+ \boldsymbol{v}_{dq}\tag{5}$$

とし，(5)式を計算していくと(6)式のようになります．

$$\begin{align}\boldsymbol{e}_{dq} &= L \boldsymbol{R}^T(\omega t)\frac{d}{dt}\{\boldsymbol{R}(\omega t)\boldsymbol{i}_{dq}\}+ R\boldsymbol{i}_{dq}+ \boldsymbol{v}_{dq} \\ &= L \boldsymbol{R}^T(\omega t)\left\{\boldsymbol{R}(\omega t) \frac{d\boldsymbol{i}_{dq}}{dt} + \frac{d}{dt} \boldsymbol{R}(\omega t)\boldsymbol{i}_{dq}\right\}+ R\boldsymbol{i}_{dq}+ \boldsymbol{v}_{dq} \\ &= L\left\{\frac{d\boldsymbol{i}_{dq}}{dt}+\left[\begin{array}{cc}\cos{\omega t} & \sin{\omega t} \\ -\sin{\omega t} & \cos{\omega t}\end{array}\right]\cdot \omega \left[\begin{array}{cc}-\sin{\omega t} & -\cos{\omega t} \\ \cos{\omega t} & -\sin{\omega t}\end{array}\right] \boldsymbol{i}_{dq}\right\}+R\boldsymbol{i}_{dq}+\boldsymbol{v}_{dq} \\ &= L\left(\frac{d\boldsymbol{i}_{dq}}{dt}+\omega \boldsymbol{J}\boldsymbol{i}_{dq}\right)+R\boldsymbol{i}_{dq}+\boldsymbol{v}_{dq}\end{align} \tag{6}$$

(6)式より，(7)式のようにを状態変数とする状態方程式が成り立ちます．

$$\frac{d\boldsymbol{i}_{dq}}{dt}=-\left(\frac{R}{L}\boldsymbol{I}+\omega\boldsymbol{J}\right)\boldsymbol{i}_{dq}-\frac{1}{L}\boldsymbol{v}_{dq}+\frac{1}{L}\boldsymbol{e}_{dq}\tag{7}$$

電源電圧は外乱であるためとして(7)式をラプラス変換し，を入力，を出力とする，すなわちとなる伝達関数行列を求めると(8)式となります．

$$\begin{align}\boldsymbol{P}(s)&=-\frac{1}{L}\left\{\left(s+\frac{R}{L}\right)\boldsymbol{I}+\omega \boldsymbol{J}\right\}^{-1} \\ &= -\frac{1}{L}\left[\begin{array}{cc} s+\frac{R}{L} & -\omega \\ \omega &  s+\frac{R}{L} \end{array}\right]^{-1}\end{align}\tag{8}$$

また，(8)式の伝達関数行列の逆行列より，入出力の関係を反転させると(9)式となります．

$$\begin{align}\boldsymbol{P}^{-1}(s)&= -L\left[\begin{array}{cc} s+\frac{R}{L} & -\omega \\ \omega &  s+\frac{R}{L} \end{array}\right] \\ &= -\left[\begin{array}{cc} Ls+R & -\omega L \\ \omega L &  Ls+R \end{array}\right]\end{align}\tag{9}$$

(9)式をブロック線図で表現すると図3のように表されます．ただし，信号の流れは右側から左側に向かうものとして表しています．

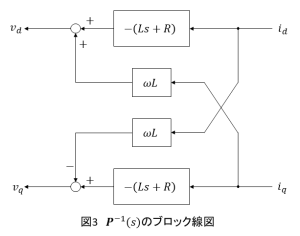
図3のブロック線図より，改めて入出力の関係をもとに戻すように変形させると，図4のブロック線図となります．

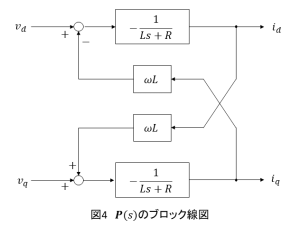
また，電源電圧,を追加すると図5となり，これをdq座標系上でのPWMコンバータのプラントモデルとして扱います．

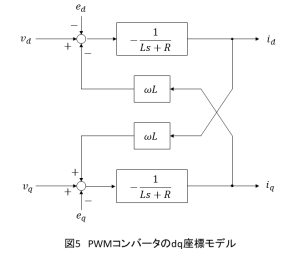
電流制御系の構成

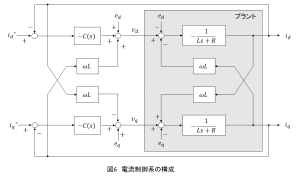
図5のようにモデル化されたdq座標系上のPWMコンバータに対して，を操作することでを制御するための電流制御器を構成します．プラントのブロック線図からわかる通り，d軸とq軸の間で互いに外乱として干渉し合っています．また，電源電圧も外乱として含まれています．それらを相殺するような形でフィードフォワード制御を考えると，図6のような制御系が構成されます．

これは，図7と等価になります．このように，それぞれの干渉を無くし，各軸で独立した制御系として扱うことができます．この制御手法は非干渉制御と呼ばれます．ベクトル制御を構成する上で必須ではありませんが，一方の軸電流の指令値を急変させた際の，もう一方の軸電流の変動を抑制することができます．

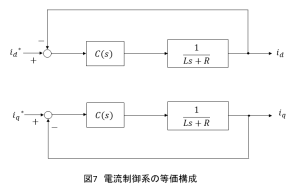
d軸とq軸は全く同じ系(非突極性)ですので，それぞれの軸の電流制御器も同じパラメータで設計すればよいことになります．電流制御器には一般的に(10)式で示されるようにPI制御が使われます．プラントの伝達関数と制御器のパラメータの設計については以前の記事と同様ですので，そちらを参照してください．

$$\begin{align}C(s)&=K_p\left(1+\frac{1}{T_is}\right) \\ &=\omega_c L\left(1+\frac{R}{Ls}\right)\end{align}\tag{10}$$

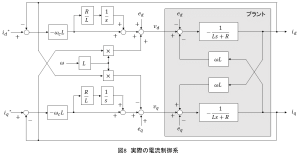
クロスオーバ角周波数をとし，最終的に図8のように電流制御系が構成されます．

二次一般化積分器ベース位相同期ループ

以前の記事でも紹介したように，位相同期ループ(PLL)は電源電圧の正弦波信号からその位相角と角周波数を得ることができるものです．二次一般化積分器ベースPLL(SOGI-based PLL)では，それらに加え電源電圧に対し位相が90°遅れた信号と，電源電圧をdq変換し直流とした信号も得ることができます．つまり，単相の電源電圧をとして与えると，，，も推定できるというものです．

まず，SOGI部分の構成について考えてみます．
二相の電源電圧を(11)式のように仮定します．

$$\boldsymbol{e}_{\alpha\beta}=E_m\left[\begin{array}{c}\cos{\omega t}  \\ \sin{\omega t}\end{array}\right]\tag{11}$$

これを微分すると(12)式となります．

$$\begin{align}\frac{d\boldsymbol{e}_{\alpha\beta}}{dt} &= E_m\omega \left[\begin{array}{c} -\sin{\omega t}  \\ \cos{\omega t}\end{array}\right] \\ &=E_m\omega \boldsymbol{J}\left[\begin{array}{c} \cos{\omega t}  \\ \sin{\omega t}\end{array}\right]\end{align}\tag{12}$$

したがって，(13)式のような状態方程式が成り立ちます．

$$\frac{d\boldsymbol{e}_{\alpha\beta}}{dt} = \omega \boldsymbol{J}\boldsymbol{e}_{\alpha\beta}\tag{13}$$

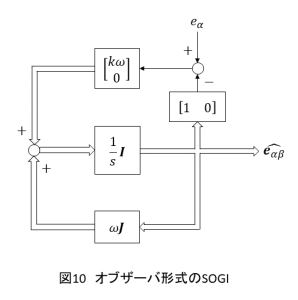
(13)式より，は既知であることからそれを出力とし，をオブザーバゲインとして同一次元状態オブザーバを構成すると(14)式となります．

$$\frac{d\hat{\boldsymbol{e}_{\alpha\beta}}}{dt} = \omega \boldsymbol{J}\hat{\boldsymbol{e}_{\alpha\beta}}+\boldsymbol{l}(e_\alpha-\left[\begin{array}{cc} 1 & 0 \end{array} \right]\hat{\boldsymbol{e}_{\alpha\beta}})\tag{14}$$

これにより，を与えることでそれに対し位相が遅れたを推定することができます．
オブザーバゲインをとすると，(14)式より(15)式となります．

$$\begin{align}\frac{d\hat{\boldsymbol{e}_{\alpha\beta}}}{dt} &= \omega \boldsymbol{J} \hat{\boldsymbol{e}_{\alpha\beta}} + \left[\begin{array}{c} k \omega  \\ 0 \end{array}\right] (e_\alpha-\left[\begin{array}{cc} 1 & 0 \end{array} \right]\hat{\boldsymbol{e}_{\alpha\beta}}) \\ &= \left[\begin{array}{cc} -k \omega & -\omega \\ \omega &  0 \end{array}\right] \hat{\boldsymbol{e}_{\alpha\beta}}+\left[\begin{array}{c} k\omega  \\ 0 \end{array}\right] e_{\alpha} \end{align}\tag{15}$$

(15)式より，伝達関数を(16)式のように求めます．

$$\begin{align}\frac{\hat{\boldsymbol{e}_{\alpha\beta}}(s)}{e_\alpha(s)}&= \left(s\boldsymbol{I}-\left[\begin{array}{cc} -k \omega & -\omega \\ \omega &  0 \end{array}\right]\right)^{-1}\left[\begin{array}{c} k\omega  \\ 0 \end{array}\right]  \\ &= \left[\begin{array}{cc} s + k \omega & \omega \\ -\omega &  s \end{array}\right]^{-1}\left[\begin{array}{c} k\omega  \\ 0 \end{array}\right] \\ &= \frac{1}{s^2+k\omega s+\omega^2}\left[\begin{array}{cc} s & -\omega \\ \omega &  s + k \omega \end{array}\right]\left[\begin{array}{c} k\omega  \\ 0 \end{array}\right] \\ &= \frac{1}{s^2+k\omega s+\omega^2}\left[\begin{array}{c} k\omega s \\ k\omega^2 \end{array}\right]\end{align}\tag{16}$$

(16)式から，はを通過角周波数とするBPF，はを遮断角周波数とする二次LPFとなっていることがわかります．すなわち，SOGIの本質は単なるフィルタであるといえます．
また，に依らす(17)～(20)式が成り立ちます．

$$\left|\frac{\hat{e_\alpha}(j\omega)}{e_\alpha(j\omega)}\right|=1\tag{17}$$$$\arg\left(\frac{\hat{e_\alpha}(j\omega)}{e_\alpha(j\omega)}\right)=0\tag{18}$$$$\left|\frac{\hat{e_\beta}(j\omega)}{e_\alpha(j\omega)}\right|=1\tag{19}$$$$\arg\left(\frac{\hat{e_\beta}(j\omega)}{e_\alpha(j\omega)}\right)=-\frac{\pi}{2}\tag{20}$$

それぞれのボード線図を描くと図9のようになります．

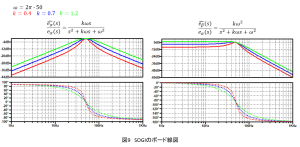
このように，電源電圧から同位相の基本波と，それと同振幅で位相が遅れたものが取得されます．これらは即ちそれぞれ，に該当するものであるとわかります．
上記のように図10のオブザーバとして考えることができるSOGIですが，一般的に図11のように構成されます．それぞれは等価となります．

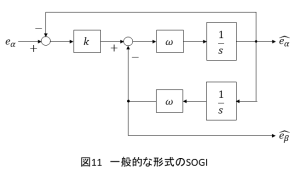
SOGIに対しdq変換とPLLを組み合わせ，SOGI-based PLLが構成されます．SOGIにより得られた固定座標系の電源電圧を，PLLで推定されている位相角に基づいてdq変換します．PLLから得られる位相角の推定値は，(21)式のように目標の位相角からだけずれています．

$$\hat{\theta}=\theta^{\ast}-\Delta\theta\tag{21}$$

が目標の位相角に基づき(22)式とする場合，は(23)式となります．

$$\begin{align}\hat{\boldsymbol{e}_{\alpha\beta}} &= E_m\left[\begin{array}{c}\cos{\theta ^{\ast}} \\ \sin{\theta ^{\ast}}\end{array}\right] \\ &= E_m\left[\begin{array}{c}\cos{(\hat{\theta}+\Delta\theta)} \\ \sin{(\hat{\theta}+\Delta\theta)}\end{array}\right] \end{align}\tag{22}$$

$$\begin{align}\hat{\boldsymbol{e}_{dq}} &=\boldsymbol{R}^T(\hat{\theta})\hat{\boldsymbol{e}_{\alpha\beta}} \\ &= E_m\left[\begin{array}{cc}\cos{\hat{\theta}} & \sin{\hat{\theta}} \\ -\sin{\hat{\theta}} & \cos{\hat{\theta}}\end{array}\right]\left[\begin{array}{c}\cos{(\hat{\theta}+\Delta\theta)} \\ \sin{(\hat{\theta}+\Delta\theta)}\end{array}\right] \\ &= E_m \left[\begin{array}{c}\cos{\Delta\theta} \\ \sin{\Delta\theta}\end{array}\right]\end{align}\tag{23}$$

したがって，(24)式により位相角の誤差であるが得られます．ただし，実装する際はatan2関数を使用します．

$$\Delta\theta = \tan^{-1}\left(\frac{\hat{e_q}}{\hat{e_d}}\right)\tag{24}$$

また，が0の近傍であると考えると，(25)式のように近似することができます．

$$\Delta\theta \simeq \frac{\hat{e_q}}{\hat{e_d}}\tag{25}$$

PLLは位相角の誤差をゼロとするような制御ループです．すなわち，を指令値とみなし，をフィードバックしてその差をゼロにするような制御系を構成します．図12に示すように制御器にはPI制御を使用し，それに加え積分器を設けます．

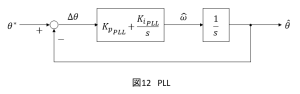
PI制御器に加え積分器を設ける理由は，位相角がランプ関数とするとの要素を持つ指令値となり，内部モデル原理によりループ内にもの要素を含まないと誤差をゼロにできないためです．また，積分器の出力がであるため，その微分である角周波数も副作用的に得ることができます．
ところで，を入力，を出力とする伝達関数を求めると(26)式となります．

$$\frac{\hat{\theta}(s)}{\theta^{\ast}(s)}=\frac{K_{p_{PLL}}s+K_{i_{PLL}}}{s^2+K_{p_{PLL}}s+K_{i_{PLL}}}\tag{26}$$

(26)式より，二次LPFとBPFの並列結合と等価であることがわかります．すなわち，PLLの本質は単なるフィルタであるといえます．ただし微分演算を用いることなく電源の角周波数を得るためには，このフィードバック制御系のような構成のPLLが有用となります．

PI制御器のパラメータ，の設計します．ループのクロスオーバ角周波数に基づき，位相余裕を確保するためその1/5にPI制御器の零点を配置すると考えると，(27)式が成り立ちます．

$$\frac{\omega_{c_{PLL}}}{5}=\frac{K_{i_{PLL}}}{K_{p_{PLL}}}\tag{27}$$

また，クロスオーバ角周波数に関して，とし開ループゲインを1とすると(28)式が成り立ちます．

$$\begin{align}\left|\left(K_{p_{PLL}}+\frac{K_{i_{PLL}}}{j\omega_{c_{PLL}}}\right)\frac{1}{j\omega_{c_{PLL}}}\right|&=\frac{\sqrt{(\omega_{c_{PLL}}K_{p_{PLL}})^2+K_{i_{PLL}}^2}}{\omega_{c_{PLL}}^2} \\ &= 1\end{align}\tag{28}$$

(27)式，(28)式より，PI制御器のパラメータは(29)式，(30)式のように求められます．

$$\begin{align}K_{p_{PLL}}&=\frac{5}{\sqrt{26}}\omega_{c_{PLL}} \\ &\approx \omega_{c_{PLL}}\end{align}\tag{29}$$

$$\begin{align}K_{i_{PLL}}&= \frac{\omega_{c_{PLL}}^2}{\sqrt{26}} \\ &\approx \frac{\omega_{c_{PLL}}^2}{5}\end{align}\tag{30}$$

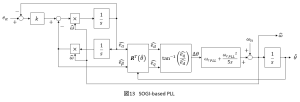
以上より，SOGI-based PLLを構成すると図13のようになります．PLLから得られる角周波数をSOGIに与えます．の初期値がゼロであると始動できないため，予め電源周波数に基づきをフィードフォワード的に与えます．
また，位相角を無限大に増加させるような処理は実際にはできないため，PLLの積分器をの範囲で回転させる必要があります．

仮想軸エミュレーション

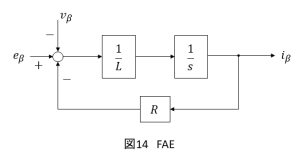
単相PWMコンバータでは，α軸電流だけは得られるものの，それに対し位相が90°遅れた相のβ軸電流が実在しません．オールパスフィルタやヒルベルト変換によりα軸電流の位相を90°遅らせることで仮のβ軸電流を作る方法がありますが，制御の応答性に難があります．
そこで，もう一相分のPWMコンバータの回路(プラント)を仮想的に制御系内に作り，β軸電流を得ることができる仮想軸エミュレーション(FAE)が提案されています．この方法では事実上の二相PWMコンバータと同様の構成となるため，高速な応答性が得られます．

(1)式より，β軸のプラントは(31)式のようなモデルとなります．

$$e_\beta =L\frac{di_\beta}{dt}+Ri_\beta + v_\beta \tag{31}$$

(31)式をラプラス変換し，について求めると，(32)式となります．

$$i_\beta(s)=\frac{1}{Ls+R}\{e_\beta(s)-v_\beta(s)\}\tag{32}$$

はSOGI-based PLLより得られ，または電流制御器の出力を逆dq変換して得られるものです．それらの差分をという一次のLPFを通してが求められるということになります．すなわち，FAEの本質は単なるフィルタであるといえます．FAEをブロック線図に表すと図14のようになります．

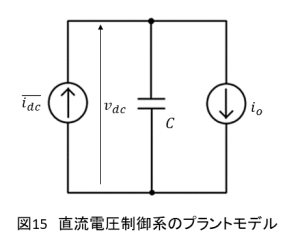
直流電圧制御系

PWMコンバータは有効電力成分を操作することにより，直流側の電圧を一定に制御します．dq座標系において，有効電力pは(33)式で表されます．

$$p=\frac{e_di_d}{2}\tag{33}$$

直流側は電流源と平滑コンデンサにより，図15のように簡単なモデルで表すことができます．したがって直流電圧制御系は，制御器の出力をとし，平滑コンデンサをプラントとして設計します．負荷電流は外乱とみなせます．

コンバータが出力する平均電流と直流電圧より，入力の有効電力pと出力電力が等しいと考えると，(34)式が成り立ちます．

$$p=v_{dc}\bar{i_{dc}}\tag{34}$$

(33)式，(34)式より，d軸電流の指令値と制御量が一致するとしてとすると，からへの変換則は(35)式となります．

$$i_d^{\ast}=\frac{2v_{dc}}{e_d}\bar{i_{dc}}\tag{35}$$

制御器には，クロスオーバ周波数が10Hz程度となるように設計したアンチワインドアップ付きPI制御やType2補償器，あるいは以前の記事でも紹介したデッドビート制御などを適用します．

制御系の全体構成

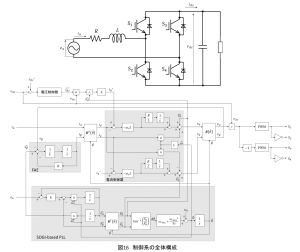
以上より，ベクトル制御を適用した単相PWMコンバータの制御系を構成すると図16のようになります．

また，電源電圧の取得に電源電圧オブザーバを用いることで，電源電圧センサレス化も可能です．

作例

製作した単相PWMコンバータの各パラメータの設定値を表1に示します．

単相PWMコンバータの電源電圧センサレス仮想軸電流ベクトル制御を実装できました。
d軸電流(有効電流)により直流出力電圧を一定制御しつつ、q軸電流(無効電流)の指令値を外部から与えている様子です。 https://t.co/91274Uc9fS pic.twitter.com/mRq4p75ufK

— タマゴさん (@86723nasogamat) November 13, 2022

まとめ

単相PWMコンバータにベクトル制御を適用するにあたって，その基本手法を紹介しました．ここで紹介したSOGI-based PLLやFAEなどについて国内の文献はほとんど無いため，パワエレ制御初学者を含み広く知られていただけたら幸いです．