幼女でも作れるPWMコンバータ

三相ACモータの多くは三相AC200Vや三相AC400Vなどが定格電圧となっているため，それを駆動するインバータ用の直流電源にはそれ相応の高い電圧が必要となります．一般家庭用の商用電源電圧は単相AC100Vであり，これを整流し，かつ昇圧するような回路が求められます．それを実現するような回路のひとつとして，倍電圧整流回路が挙げられます．倍電圧整流回路は部品数が少なく，非常に容易に構成が可能ですが，任意の出力電圧が得られない(AC100V入力の場合約DC280Vのみ)，入力電流がパルス状になるため力率が悪く，高調波の影響で系統中の機器に悪影響を及ぼす可能性がある，などの問題があります．

これらの問題を解決するにはPFC(力率補正)回路が有用です．一般的なPFCは，ブリッジダイオードによる全波整流回路の後段に昇圧チョッパを設けた形であり，入力電流を正弦波状となるように昇圧チョッパを制御しつつ出力電圧を任意の値に昇圧するような動作が可能です．ただし，全波整流回路や昇圧チョッパに対して，電流が導通する際の素子数が多くなるため，電力損失が増加しやすくなります．また，倍電圧整流回路や一般的なPFCなどの，ダイオードによる整流作用のみを用いて構成した整流回路では，モータの回生電力を系統側に返すような逆方向の動作ができません．

そのような観点からさらに改良を加えた整流回路として，スイッチング素子でフルブリッジ回路を構成しAC入力側にリアクトルを設けたようなPWM整流器，あるいはPWMコンバータがあります．PWMにより制御されるコンバータというやや抽象的な呼ばれ方であり，先に示したPFC回路もPWMコンバータの一種ではある(逆も然り)と言えますが，一般的にPWMコンバータというとこの構成の整流回路を指すことが多いようです．この回路では入力電流の制御により力率の補正は勿論のこと，系統連系インバータとしての動作もできるため，モータの回生電力を系統側に返すというような回生動作も可能となります．

ここでは，単相交流電源を入力とするPWMコンバータの制御系の構成方法を主として，その作例を紹介します．

目次

• 1. 制御系の基本構成
• 2. 実際の制御系
• 3. 電流制御器
  • 3-1. プラントの伝達関数
  • 3-2. 制御器の設計
• 4. 電源電圧オブザーバ
  • 4-1. 0次外乱オブザーバ
  • 4-2. 周期外乱オブザーバ
• 5. 電圧制御器
  • 5-1. プラントの離散時間モデル
  • 5-2. デッドビート制御器の構成
  • 5-3. 安定性
• 6. PLL
  • 6-1. デッドビートPLL
  • 6-2. 適応PLL
• 7. 起動方法
• 8. 制御プログラムの構成
• 9. 製作
• 10. 動作確認
• 11. まとめ

1. 制御系の基本構成

単相PWMコンバータの制御系は基本的に図1のように構成されます．ブロック線図中のConverterが回路図で示されるようなプラントとなります．フルブリッジ回路のスイッチに対するPWMのDuty比をプラントへの入力，交流側の入力電流と直流側の出力電圧を状態あるいは出力，電源電圧と負荷電流を外乱とみなすことができます．入力電流を制御するマイナーループと，出力電圧を制御するメジャーループからなるカスケード制御となっています．入力電流を電源電圧と同相(力率1の場合)の正弦波となるようにACR(Auto Current Regulator:電流制御器)で制御しつつ，その振幅をAVR(Auto Voltage Regulator:電圧制御器)により調整することで出力電圧を制御します．また，電流制御系に与える指令値の基となる，電源電圧と同期した正弦波をPLL(Phase Locked Loop:位相同期器)により生成します．

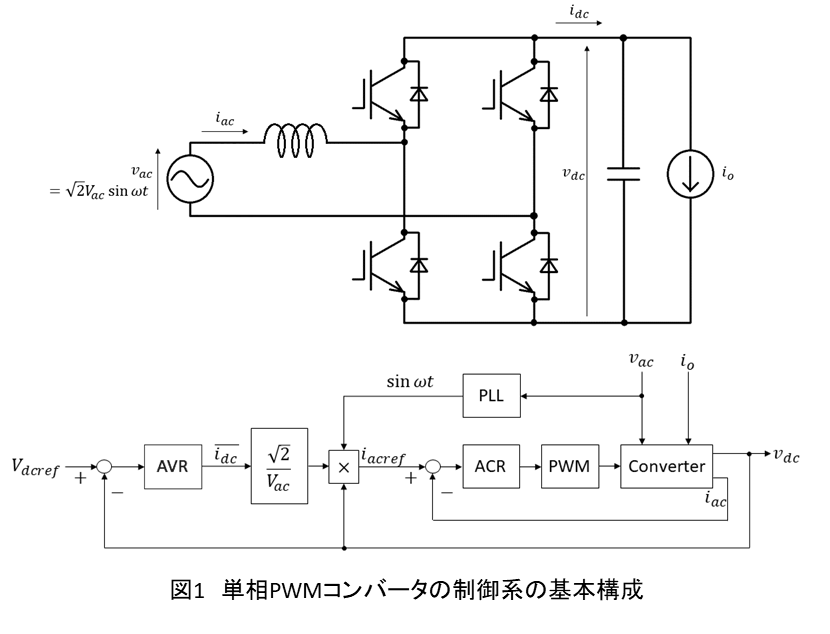
電圧制御器から出力される操作量は，平滑コンデンサに流れる電流と負荷電流を合わせた出力電流の平均的な値に相当します．電源電圧の実効値と入力電流の実効値より，入出力電力が等しいとすると(1)式が成り立ちます．
$$V_{ac}I_{ac}=v_{dc}\overline{i_{dc}}\tag{1}$$
また，とすると(2)式が成り立ちます．
$$I_{ac}=\frac{i_{acref}}{\sqrt{2}\sin{\omega t}}\tag{2}$$
(2)式を(1)式に代入すると(3)式となります．
$$V_{ac}\frac{i_{acref}}{\sqrt{2}\sin{\omega t}}=v_{dc}\overline{i_{dc}}\tag{3}$$
(3)式よりについて解くと(4)式となります．
$$i_{acref}=\frac{\sqrt{2}v_{dc}\sin{\omega t}}{V_{ac}}\overline{i_{dc}}\tag{4}$$
従って，図1におけるブロック線図と等価となることが示されます．

2. 実際の制御系

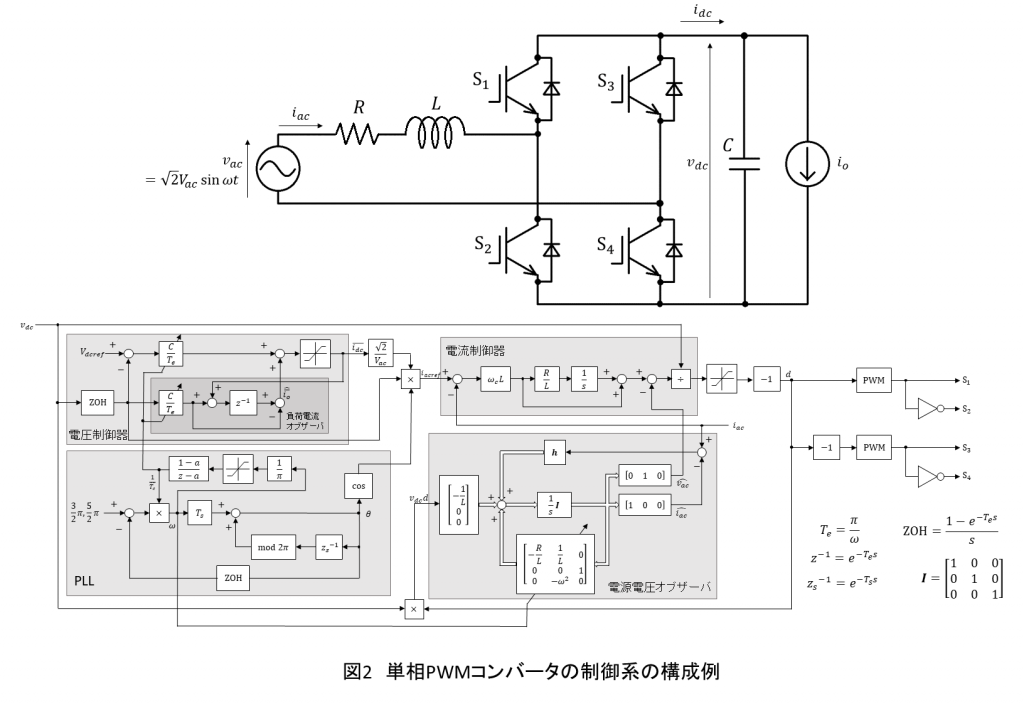
単相PWMコンバータの制御系の一例として，ここでは図2のようなシステムについて取り上げ，その理論や設計方法を述べていきます．マイコンによるディジタル制御を想定していますが，図2におけるブロック線図では，サンプリングによるゼロ次ホールドと，演算時間によるむだ時間遅延は省略しています．

このシステムにおいてコンバータの制御に必要なセンサは，入力電流を検出する電流センサと，出力電圧を検出する電圧センサとなります．一般的に電源電圧を検出する電圧センサも使われることが多々ありますが，ここではオブザーバにより推定することを考え，電源電圧センサレスとします．また，無効電力補償などは含めず，常に電源電圧と入力電流を同相とし力率1で動作させることとします．

ここではをコンバータを駆動するPWMのDuty比として扱いますが，フルブリッジのレグ間のパルス電圧波形を考え，定義域を-1から1(PWM搬送波の振幅範囲を-1から1)とします．のとき，スイッチ–はDuty比0.5で駆動されますが，フルブリッジのレグ間電圧は0となります．

は制御周期(サンプリング周期)，または電源電圧の半周期を示します．それらに応じては制御周期に対する遅延器，は電源電圧の半周期に対する遅延器となります．遅延器とゼロ次ホールドは，電源電圧のゼロクロス点と同期して動作させます．

3. 電流制御器

3-1. プラントの伝達関数

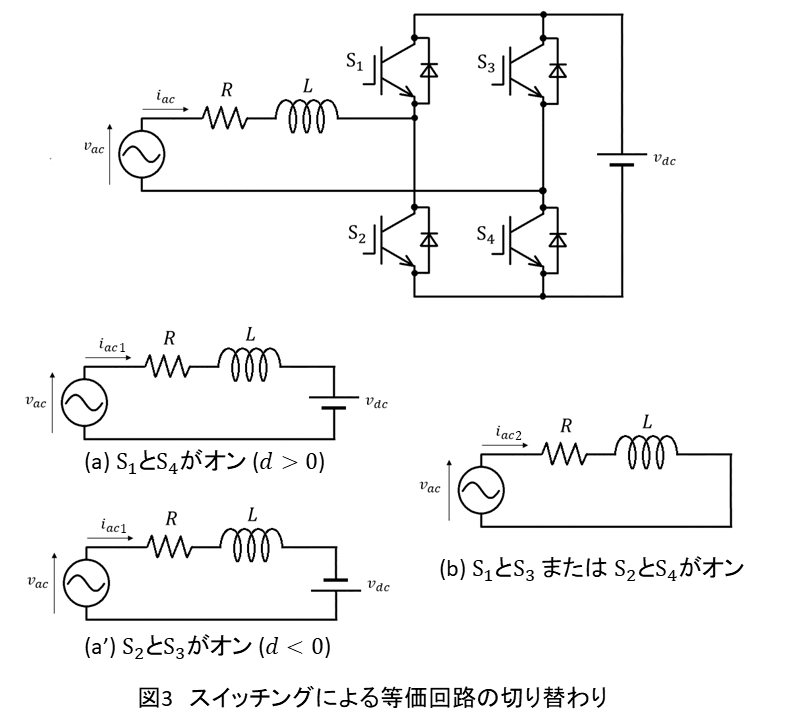
電流制御器を設計するために，まずはそのプラントのモデル化を行います．図3のように，PWMによるスイッチングによって交流側は2つの等価回路が交互に切り替わるため，これらの状態方程式を立式してからDuty比で重み付け平均するような状態平均化法を適用します．のときは図3の(a)と(b)，のときは(a’)と(b)の等価回路がスイッチングにより切り替わります．

の場合を考えます．図3(a)の回路の電圧方程式は(5)式となります．
$$v_{ac}-v_{dc}=Ri_{ac1}+L\frac{di_{ac1}}{dt}\tag{5}$$
(5)式よりを状態変数とすると，状態方程式は(6)式となります．
$$\frac{di_{ac1}}{dt}=-\frac{R}{L}i_{ac1}+\frac{1}{L}v_{ac}-\frac{1}{L}v_{dc}\tag{6}$$
また，図3(b)の回路の電圧方程式は(7)式となります．
$$v_{ac}=Ri_{ac2}+L\frac{di_{ac2}}{dt}\tag{7}$$
(7)式よりを状態変数とすると，状態方程式は(8)式となります．
$$\frac{di_{ac2}}{dt}=-\frac{R}{L}i_{ac2}+\frac{1}{L}v_{ac}\tag{8}$$
(6)式に，(8)式にを掛け重み付け平均をとり，状態変数をとすると(9)式の状態平均化方程式が導出されます．
$$\frac{di_{ac}}{dt}=-\frac{R}{L}i_{ac}+\frac{1}{L}v_{ac}-\frac{1}{L}v_{dc}d\tag{9}$$
またの場合，図3(a’)と(b)の回路から，それぞれ，の重み付け平均により状態方程式を導出しても(9)式と同様となります．
出力電圧は一定とみなしを定数として(9)式をラプラス変換すると(10)式となります．
$$si_{ac}(s)=-\frac{R}{L}i_{ac}(s)+\frac{1}{L}v_{ac}(s)-\frac{1}{L}v_{dc}d(s)\tag{10}$$
(10)式より，について求めると(11)式となります．
$$i_{ac}(s)=-\frac{1}{Ls+R}\left\{v_{dc}d(s)-v_{ac}(s)\right\}\tag{11}$$
(11)式より，外乱としてとし，入力を，出力をとすると，(12)式のような伝達関数が成り立ち，これが電流制御系におけるプラントとなります．
$$P_c(s)=\frac{i_{ac}(s)}{v_{dc}d(s)}=-\frac{1}{Ls+R}\tag{12}$$

3-2. 制御器の設計

電流制御器は(13)式の伝達関数で示されるようなPI制御器を基本として構成し，比例ゲインと積分時間を設計します．
$$C_{pi}(s)=K_p\left(1+\frac{1}{T_is}\right)=K_p\frac{T_is+1}{T_is}\tag{13}$$
プラントにおける位相遅れを制御器により補償するため，プラントの極と制御器の零点を相殺させるように積分時間を決定します．(12)式より，の極は，の零点はとなるため，は(14)式のように求まります．
$$T_i=\frac{L}{R}\tag{14}$$
従って，(14)式を(13)式に代入すると(15)式となります．
$$C_{pi}(s)=K_p\frac{Ls+R}{Ls}\tag{15}$$
電流制御ループの一巡伝達関数を考えると，(16)式となります．
$$-C_{pi}(s)P_c(s)=\frac{K_p}{Ls}\tag{16}$$
一巡伝達関数におけるゲインが1となる角周波数(クロスオーバー角周波数)をとすると，(17)式が成り立ちます．
$$|-C_{pi}(j\omega_c)P_c(j\omega_c)|=\frac{K_p}{\omega_cL}=1\tag{17}$$
従って，(17)式よりが(18)式のように求まります．
$$K_p=\omega_cL\tag{18}$$
(14)式，(18)式より，PI制御による電流制御系を構成すると図4となります．プラントの伝達関数が負であるため，それに応じて制御器の出力に-1を掛けて操作量を反転させます．

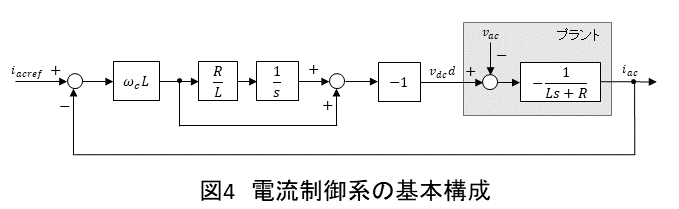
また，外乱である電源電圧を相殺するようにをフィードフォワード的に重畳すると，図5のようになります．

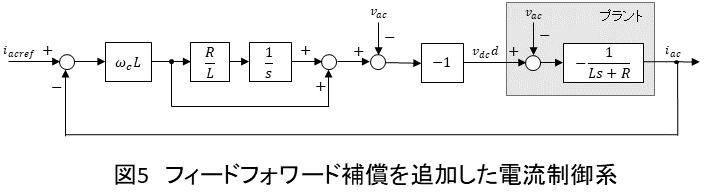
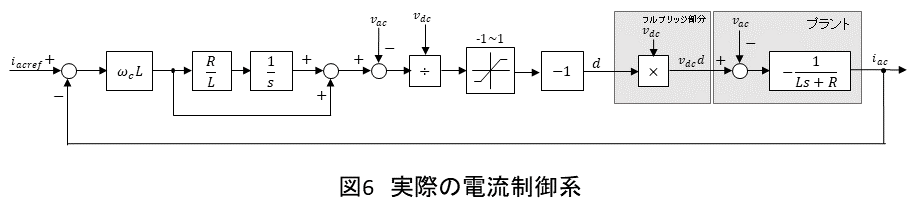
実際には，制御器の出力はPWMを介してプラントに入力するため，図6のようにで割ることでPWMのDuty比のみの信号を作ります．の定義域は-1~1であるためリミッタを設けます．コンバータのフルブリッジにおいてに再びが掛けられることになり，プラントには同様にが入力されます．

4. 電源電圧オブザーバ

外乱オブザーバを構成することで，プラントに対する入力と出力より，電源電圧を推定することができます．ここでは電源電圧を0次外乱とする場合と，周期外乱とする場合の2通りの構成方法を説明します．

4-1. 0次外乱オブザーバ

電源電圧は50Hzあるいは60Hzの正弦波ですが，これがサンプリング周波数に対して十分低いなら，電源電圧が一定値であり時間微分が0であるような外乱(0次外乱)とみなした上でオブザーバを構成することができます．オブザーバを構成するにあたり，に加えを状態変数とした拡大系の状態空間モデルを考えます．

に関する状態方程式である(9)式を再掲します．
$$\frac{di_{ac}}{dt}=-\frac{R}{L}i_{ac}+\frac{1}{L}v_{ac}-\frac{1}{L}v_{dc}d\tag{9}$$
また，を0次外乱とするため，(19)式となります．
$$\frac{dv_{ac}}{dt}=0\tag{19}$$
(9)式，(19)式より，(20)式のような拡大系の状態方程式が成り立ちます．
$$\frac{d}{dt}\left[\begin{array}{c}i_{ac} \\ v_{ac} \end{array} \right] = \left[\begin{array}{cc}-\frac{R}{L} & \frac{1}{L} \\ 0 & 0 \end{array} \right]\left[\begin{array}{c}i_{ac} \\ v_{ac} \end{array} \right] + \left[\begin{array}{c}-\frac{1}{L} \\ 0 \end{array} \right]v_{dc}d \tag{20}$$
また，出力方程式は(21)式となります．
$$i_{ac}=\left[\begin{array}{cc} 1 & 0 \end{array} \right]\left[\begin{array}{c}i_{ac} \\ v_{ac} \end{array} \right] \tag{21}$$
(20)式，(21)式より，(22)式のように同一次元状態オブザーバを構成します．，はそれぞれ，の推定値，はオブザーバゲインを表します．
$$\frac{d}{dt}\left[\begin{array}{c}\widehat{i_{ac}} \\ \widehat{v_{ac}} \end{array} \right] = \left[\begin{array}{cc}-\frac{R}{L} & \frac{1}{L} \\ 0 & 0 \end{array} \right]\left[\begin{array}{c}\widehat{i_{ac}} \\ \widehat{v_{ac}} \end{array} \right] + \left[\begin{array}{c}-\frac{1}{L} \\ 0 \end{array} \right]v_{dc}d+\boldsymbol{h}(i_{ac}-\widehat{i_{ac}}) \tag{22}$$
の固有値の実部が負となるようにオブザーバゲインを設計(極配置)することで，オブザーバは安定となります．

例として，カットオフ角周波数の2次のバターワース多項式である(23)式の根にオブザーバの極を配置します．
$$\left(\frac{s}{\omega_{oc}}\right)^2+\frac{\sqrt{2}s}{\omega_{oc}}+1=0\tag{23}$$

4-2. 周期外乱オブザーバ

電源電圧を0次外乱としてオブザーバを構成する場合，サンプリング周波数が低いほど真値に対する推定値の位相遅れが顕著になります．電源電圧が一定周期の正弦波とするような周期外乱モデルからオブザーバを構成することで，より真値に対する推定値の追従性を向上させることができます．

とし，の2階微分について考えると(24)式が成り立ちます．
$$\begin{align}\frac{d^2v_{ac}}{dt^2}&=-\omega^2A\sin{\omega t}\\&=-\omega^2v_{ac}\end{align}\tag{24}$$
とすると(24)式より(25)式，(26)式となります．
$$\frac{dv_{ac}}{dt}=\dot{v_{ac}}\tag{25}$$$$\frac{d\dot{v_{ac}}}{dt}=-\omega^2v_{ac}\tag{26}$$
(9)式，(25)式，(26)式より，(27)式のような拡大系の状態方程式が成り立ちます．
$$\frac{d}{dt} \left[ \begin{array}{c} i_{ac} \\ v_{ac} \\ \dot{v_{ac}} \end{array} \right] = \left[ \begin{array}{ccc} -\frac{R}{L} & \frac{1}{L} & 0 \\ 0 & 0 & 1 \\ 0 & -\omega^2 & 0 \end{array} \right] \left[ \begin{array}{c} i_{ac} \\ v_{ac} \\ \dot{v_{ac}} \end{array} \right] + \left[ \begin{array}{c} -\frac{1}{L} \\ 0 \\ 0 \end{array} \right]v_{dc}d\tag{27}$$
また，出力方程式は(28)式となります．
$$i_{ac}=\left[\begin{array}{ccc} 1 & 0 & 0 \end{array} \right]\left[\begin{array}{c}i_{ac} \\ v_{ac} \\ \dot{v_{ac}} \end{array} \right] \tag{28}$$
(27)式，(28)式より，(29)式のように同一次元状態オブザーバを構成します．
$$\frac{d}{dt} \left[ \begin{array}{c} \widehat{i_{ac}} \\ \widehat{v_{ac}} \\ \widehat{\dot{v_{ac}}} \end{array} \right] = \left[ \begin{array}{ccc} -\frac{R}{L} & \frac{1}{L} & 0 \\ 0 & 0 & 1 \\ 0 & -\omega^2 & 0 \end{array} \right] \left[ \begin{array}{c} \widehat{i_{ac}} \\ \widehat{v_{ac}} \\ \widehat{\dot{v_{ac}}} \end{array} \right] + \left[ \begin{array}{c} -\frac{1}{L} \\ 0 \\ 0 \end{array} \right]v_{dc}d + \boldsymbol{h}(i_{ac}-\widehat{i_{ac}})\tag{29}$$
の固有値の実部が負となるようにオブザーバゲインを設計(極配置)することで，オブザーバは安定となります．

例として，カットオフ角周波数の3次のバターワース多項式である(30)式の根にオブザーバの極を配置します．
$$\left( \frac{s}{\omega_{oc}}+1 \right) \left\{ \left( \frac{s}{\omega_{oc}} \right) ^2+\frac{s}{\omega_{oc}}+1 \right\} =0 \tag{30}$$

5. 電圧制御器

電圧制御にも電流制御と同様にPI制御を適用するのが一般的ですが，ここではより優れた制御則として筆者が考案したものを説明します．

単相PWMコンバータの入力電力は電源周波数の2倍の周波数で振動するため，出力電圧にはそれに応じたリプルが現れます．電圧制御器においてそのリプルを十分減衰させなければ，電流制御における指令値にリプルが伝わり，入力電流が歪むことになります．ただし，それは電圧制御器の出力がPI制御などの連続的に変化する場合に限られます．電圧制御器の出力を，入力電流のゼロクロス点に合わせてステップ状に変化させれば，入力電流半周期内での電流指令値に歪みを無くすことができます．すなわち，電源周波数の2倍のサンプリング周波数による離散制御を適用すればよいということになります．離散制御の一手法として，有限時間で整定させるデッドビート制御により電圧制御器を構成していきます．

参考：単相PWMコンバータにおける出力電圧のデッドビート制御

5-1. プラントの離散時間モデル

デッドビート制御を構成するにあたり，電圧制御系におけるプラントのモデル化を行います．
図7に示す連続時間系での出力電流，負荷電流，出力電圧から，(31)式，(32)式，(33)式のように離散値を定義します．，は，それぞれ電源電圧の半周期内における，の平均値を表します．

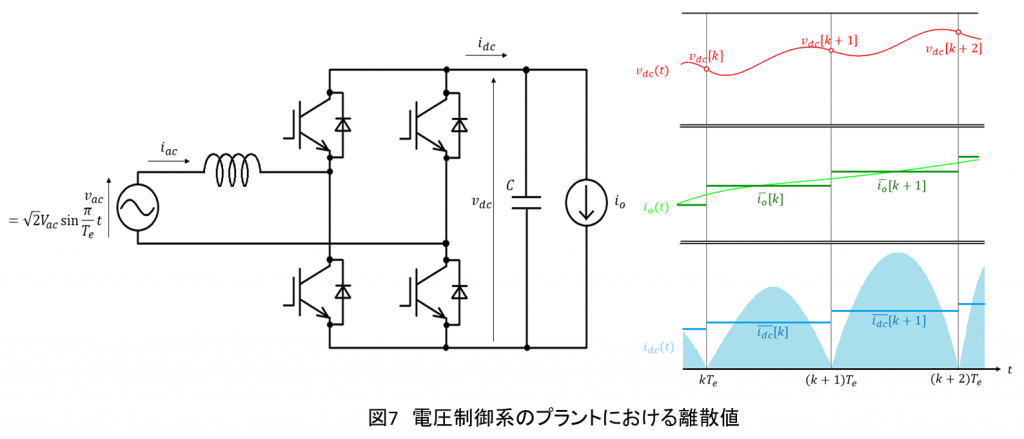
$$\overline{i_{dc}}[k]=\frac{1}{T_e}\int_{kT_e}^{(k+1)T_e}i_{dc}(t)dt\tag{31}$$$$\overline{i_o}[k]=\frac{1}{T_e}\int_{kT_e}^{(k+1)T_e}i_o(t)dt\tag{32}$$$$v_{dc}[k]=v_{dc}(kT_e)\tag{33}$$
期間の1ステップ内でコンデンサに流れる電流を考えると，1ステップにおける出力電圧の変化量を示す式として(34)式が成り立ちます．
$$\begin{align}v_{dc}\left((k+1)T_e\right)&=v_{dc}(kT_e)+\frac{1}{C}\int_{kT_e}^{(k+1)T_e}\left\{i_{dc}(t)-i_o(t)\right\}dt\\&=v_{dc}(kT_e)+\frac{T_e}{C}\left\{\frac{1}{T_e}\int_{kT_e}^{(k+1)T_e}i_{dc}(t)dt-\frac{1}{T_e}\int_{kT_e}^{(k+1)T_e}i_o(t)dt\right\}\end{align}\tag{34}$$
(31)～(34)式より，(35)式のような離散時間状態方程式が成り立ちます．これが電圧制御系におけるプラントのモデルとなります．
$$v_{dc}[k+1]=v_{dc}[k]+\frac{T_e}{C}\left(\overline{i_{dc}}[k]-\overline{i_o}[k]\right)\tag{35}$$

5-2. デッドビート制御器の構成

1ステップ先の出力電圧が指令値と一致するような操作量を求めるデッドビート制御則を考えます．従って，とし，(35)式よりについて解くと，(36)式となります．
$$\overline{i_{dc}}[k]=\frac{C}{T_e}(V_{dcref}[k]-v_{dc}[k])+\overline{i_o}[k]\tag{36}$$
負荷電流が必要となりますが，外乱オブザーバにより推定することができます．0次外乱としてとし，(35)式よりについて解くと(37)式となります．
$$\widehat{\overline{i_o}}[k+1]=\frac{C}{T_e}(v_{dc}[k]-v_{dc}[k+1])+\overline{i_{dc}}[k]\tag{37}$$
(37)式の各項を1ステップ減ずると(38)式となり，これがの推定値を得る外乱オブザーバとなります．
$$\widehat{\overline{i_o}}[k]=\frac{C}{T_e}(v_{dc}[k-1]-v_{dc}[k])+\overline{i_{dc}}[k-1]\tag{38}$$
(36)式，(38)式より，とすると図8のような出力電圧デッドビート制御器が構成されます．

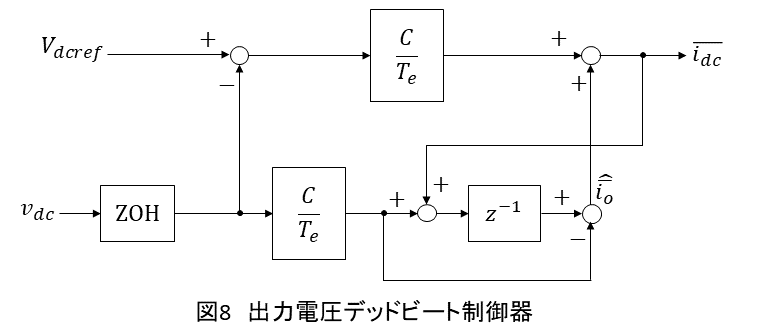
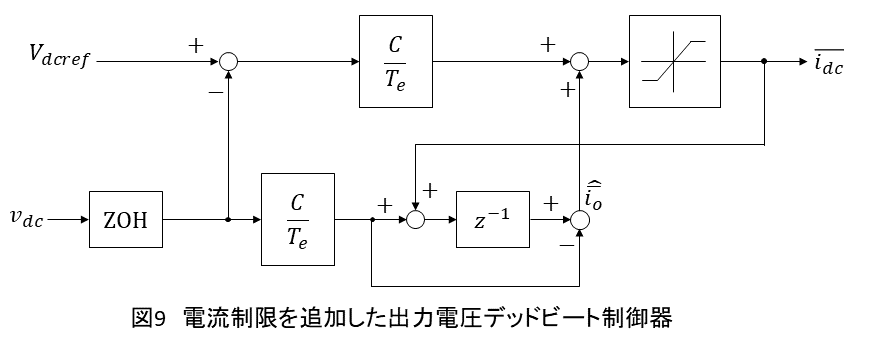
実際にはに対して電流制限をする必要があるため，図9のようにリミッタを設けます．オブザーバに与えるはプラントに入力している値そのものが必要なので，リミッタの出力側の値をオブザーバに入力します．

5-3. 安定性

上記で構成した出力電圧デッドビート制御器は，実際の平滑コンデンサ容量と電源電圧の半周期の値が必要となりますが，これらがモデルに対して誤差がある場合の安定性を考えます．電圧制御系の閉ループパルス伝達関数を求め，その特性方程式から安定条件を求めます．

(35)式のプラントの離散時間状態方程式より，外乱とすると，(39)式となります．
$$v_{dc}[k+1]=v_{dc}[k]+\frac{T_e}{C}\overline{i_{dc}}[k]\tag{39}$$
とし，(39)式をz変換すると(40)式となります．
$$zv_{dc}(z)=v_{dc}(z)+W\overline{i_{dc}}(z)\tag{40}$$
(40)式より，(41)式が成り立ちます．
$$v_{dc}(z)=\frac{W}{z-1}\overline{i_{dc}}(z)\tag{41}$$

また，(36)式と(38)式においてモデル化された値として，と置き換えると，それぞれ(42)式，(43)式となります．
$$\overline{i_{dc}}[k]=\frac{C_m}{T_{em}}(V_{dcref}[k]-v_{dc}[k])+\overline{i_o}[k]\tag{42}$$$$\widehat{\overline{i_o}}[k]=\frac{C_m}{T_{em}}(v_{dc}[k-1]-v_{dc}[k])+\overline{i_{dc}}[k-1]\tag{43}$$
，とし，(43)式を(42)式に代入すると(44)式となります．
$$\begin{align}\overline{i_{dc}}[k]&=\frac{1}{W_m}(V_{dcref}[k]-v_{dc}[k])+\frac{1}{W_m}(v_{dc}[k-1]-v_{dc}[k])+\overline{i_{dc}}[k-1]\\&=\frac{1}{W_m}(V_{dcref}[k]+v_{dc}[k-1]-2v_{dc}[k])+\overline{i_{dc}}[k-1]\end{align}\tag{44}$$
(44)式をz変換すると(45)式となります．
$$\overline{i_{dc}}(z)=\frac{1}{W_m}\left\{ V_{dcref}(z)+z^{-1}v_{dc}(z)-2v_{dc}(z) \right\}+z^{-1}\overline{i_{dc}}(z)\tag{45}$$
(45)式より，(46)式が成り立ちます．
$$\overline{i_{dc}}(z)=\frac{1}{W_m(z-1)}\left\{ zV_{dcref}(z)-(2z-1)v_{dc}(z) \right\}\tag{46}$$
(46)式を(41)式に代入すると，(47)式となります．
$$v_{dc}(z)=\frac{W}{z-1} \cdot \frac{1}{W_m(z-1)}\left\{ zV_{dcref}(z)-(2z-1)v_{dc}(z) \right\}\tag{47}$$
(47)式より，を入力，を出力とする閉ループパルス伝達関数は(48)式となります．
$$\frac{v_{dc}(z)}{V_{dcref}(z)}=\frac{Wz}{W_mz^2-2(W_m-W)z+(W_m-W)}\tag{48}$$
(48)式の特性方程式の根である極が単位円内に収まることで安定となるため，(49)式が成り立ちます．
$$\left|\frac{W_m-W\pm\sqrt{W(W-W_m)}}{W_m}\right|<1\tag{49}$$
(49)式を求めると，安定条件は(50)式となります．
$$\frac{3}{4}<\frac{W_m}{W}\tag{50}$$
従って，実際のが，モデルであるの4/3倍を超えると不安定となることが示されます．平滑コンデンサの容量が安定性に大きく影響するので，安定性を確保するならばの値をの1/5～1/10程度と小さく設定しておくことを推奨します．
なお，に対する単位ステップ応答としてを与え，最終値定理より(51)式を計算すると，モデル化誤差に依らず定常偏差は生じないことが示されます．
$$\begin{align}\lim_{k \to \infty}v_{dc}(kT_e)&=\lim_{z \to 1}\left(1-z^{-1}\right)v_{dc}(z)\\&=\lim_{z \to 1}\left(1-z^{-1}\right)V_{dcref}(z)\cdot\frac{v_{dc}(z)}{V_{dcref}(z)}\\&=\lim_{z \to 1}\left(1-z^{-1}\right)\frac{1}{1-z^{-1}}\cdot\frac{Wz}{W_mz^2-2(W_m-W)z+(W_m-W)}\\&=\frac{W}{2W_m-2W_m+W}\\&=1\end{align}\tag{51}$$

6. PLL

電流制御系への指令値を生成するために必要な電源電圧の位相角は，PLL(位相同期ループ)により取得します．アナログ制御などの簡易的なシステムでは，電源電圧そのものの振幅を調整することで直接的に電流制御系への指令値を求めることもありますが，系統中のインピーダンスによる電源電圧の歪みが起因して制御系が不安定となる可能性が高くなります．

ここでは電源電圧のゼロクロス点でのみ位相角の指令値を渡し離散的に制御されるようなPLLの構成方法について説明します．特定周波数に対して高速かつ有限時間整定できるデッドビートPLLと，それを基に構成する，周波数変動に対してゲインを適応的に補正するような適応PLLというもので，筆者が独自に考案したものです．

6-1. デッドビートPLL

PLL内の仮想的なプラントとして，位相角と角周波数より，(52)式を考えます．
$$\frac{d\theta(t)}{dt}=\omega(t)\tag{52}$$
，として，(52)式を周期で離散化すると(53)式となります．
$$\frac{\theta[k+1]-\theta[k]}{T_e}=\omega[k]\tag{53}$$
従って，(54)式のような離散時間状態方程式が成り立ちます．
$$\theta[k+1]=\theta[k]+T_e\omega[k]\tag{54}$$
とし，(54)式よりについて解くと，(55)式のようにPLLのデッドビート制御則が示されます．
$$\omega[k]=\frac{1}{T_e}(\theta_{ref}[k]-\theta[k])\tag{55}$$
(55)式より図10のように，角周波数から位相角を出力する積分器に対して，ゲインによる制御周期のフィードバック制御を構成すればよいことが示されます．これにより，指令値を与えた後にその指令値とが一致するようになります．

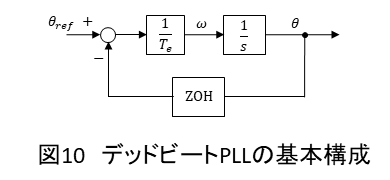
積分器の出力であるの値はまで到達したのち，0にリセットする必要があります．そのため，図11のように後退オイラー法で構成した積分器に対してを設けます．

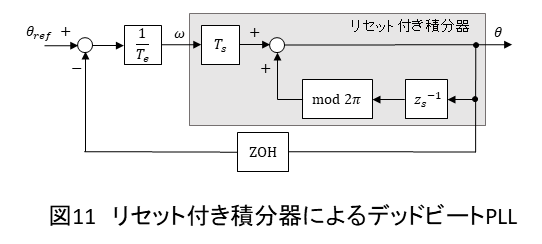
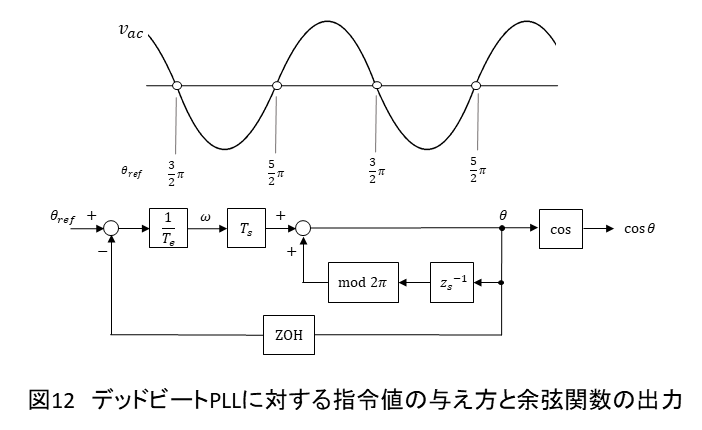
電源電圧のゼロクロス点に応じて位相角の指令値を与えるとすると，は電源電圧の半周期となり，また指令値は差分がである2つの値を交互に切り替えるような動作になります．がから0にリセットされる点で指令値を与えることを避け，かつが単調に増加するようにしなければならないため，電源電圧を余弦関数とみなし，とを指令値とします．電源電圧が減少するゼロクロス点では，増加するゼロクロス点ではを与えます．以上より，図12のようにデッドビートPLLが構成されます．

6-2. 適応PLL

電源周波数が変動する場合や，50Hzと60Hzの両方で使用する場合は，上記のデッドビートPLLにおいて制御周期が変化します．そのためゲインが一定値であると，電源電圧とPLLの位相角の間に定常偏差が生じることがあります．これを抑制するため，電源周波数の変化に対しても適応するようにゲインを可変するような構成をします．

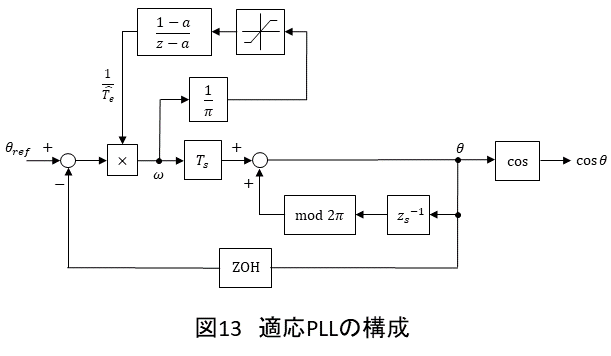
上記からわかるように，PLLでは位相角のほか角周波数を得ることができます．は電源周波数の2倍であることから，得られたからによりゲインの推定値を求めることで，漸近的に最適なゲインへ近づかせることを考えます．電源周波数の2倍の周波数が変動範囲し得る範囲をリミッタにより定め，また安定性を確保するためにフィルタを設けると図13のような適応PLLが構成されます．フィルタの出力はそのままゲインの値に該当するため，この部分は乗算と表せます．なお，フィルタのパルス伝達関数は(56)式に示すように，1次LPFと遅延器の直列接続により表されるものです．

$$\frac{1-a}{z-a}=\frac{1-a}{1-az^{-1}}z^{-1}\tag{56}$$
フィルタの定数を設計するため，適応PLLの応答を解析します．ここで，入力は位相角の指令値ではなくその角周波数にあたるとしておきます．また，PLL内の積分器はリセット機能を有しないものとし，ゲイン更新におけるリミッタも考えないものとします．したがって，図14を解析する対象のモデルとします．

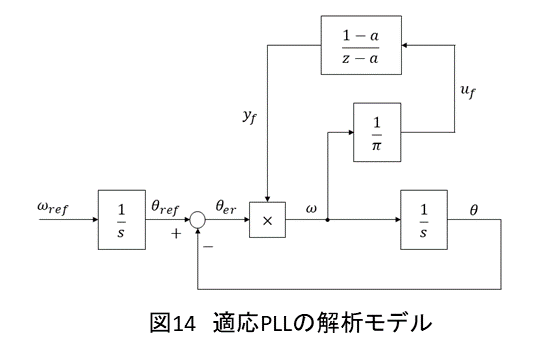
フィルタを後退オイラー法により連続系に近似し，を入力，を出力，とを状態変数とすると，(57)～(59)式のような状態空間モデルが示されます．
$$\frac{dx_f}{dt}=\frac{(1-a)(\theta_{er}-\pi)\omega_{ref}x_f}{\pi\{a\pi+(1-a)\theta_{er}\}}\tag{57}$$$$\frac{d\theta_{er}}{dt}=-\frac{a\pi x_f\theta_{er}}{a\pi+(1-a)\theta_{er}}+\omega_{ref}\tag{58}$$$$\omega=\frac{a\pi x_f\theta_{er}}{a\pi+(1-a)\theta_{er}}\tag{59}$$
(57)～(59)式は非線形であるため，定常状態近傍で線形化を行うと(60)式，(61)式となります．ただし，は微小変化量を表します．
$$\frac{d}{dt}\left[\begin{array}{c} \Delta x_f \\ \Delta \theta_{er} \end{array} \right]=\left[\begin{array}{cc} 0 & \displaystyle \frac{(1-a){\omega_{ref}}^2}{a\pi^3} \\ -a\pi & \displaystyle -\frac{a\omega_{ref}}{x} \end{array} \right]\left[\begin{array}{c} \Delta x_f \\ \Delta \theta_{er} \end{array} \right]+\left[\begin{array}{c} 0 \\ 1 \end{array} \right]\Delta\omega_{ref}\tag{60}$$$$\Delta\omega=\left[\begin{array}{cc}a\pi & \displaystyle \frac{a\omega_{ref}}{\pi} \end{array} \right]\left[\begin{array}{c} \Delta x_f \\ \Delta \theta_{er} \end{array} \right]\tag{61}$$
(60)式，(61)式より，伝達関数を求めると，(62)式となります．
$$\frac{\Delta\omega(s)}{\Delta\omega_{ref}(s)}=\frac{\displaystyle \frac{a\omega_{ref}}{\pi}s+\displaystyle \frac{(1-a){\omega_{ref}}^2}{\pi^2}}{s^2+\displaystyle \frac{a\omega_{ref}}{\pi}s+\displaystyle \frac{(1-a){\omega_{ref}}^2}{\pi^2}}\tag{62}$$
非線形状態空間モデルの導出とその線形化の計算過程についてはこちらにまとめておきます．
(62)式の特性方程式より，安定条件はとなります．また，(63)式のように2次遅れ要素標準形の分母と比較すると，固有角周波数と減衰係数は(64)式，(65)式となります．
$$s^2+\frac{a\omega_{ref}}{\pi}s+ \frac{(1-a){\omega_{ref}}^2}{\pi^2}=s^2+2\zeta \omega_ns+\omega_n^2\tag{63}$$$$\omega_n=\frac{\sqrt{1-a}\omega_{ref}}{\pi}\tag{64}$$$$\zeta=\frac{a}{2\sqrt{1-a}}\tag{65}$$
減衰係数から定数を設計する場合，(65)式よりについて求めると(66)式となります．
$$a=2\zeta\left(\sqrt{\zeta^2+1}-\zeta\right)\tag{66}$$
例として，とすると，となります．

適応PLLにより得られるやを用いて，電源電圧オブザーバ(周期外乱オブザーバ)と出力電圧デッドビート制御器のパラメータの更新を行います．

7. 起動方法

PWMコンバータに電源を投入してから安全かつ確実に起動させるためには，突入電流の防止や電源電圧の位相検出などの処理が必要となります．PWMコンバータの起動時のフローチャートを図15に示します．

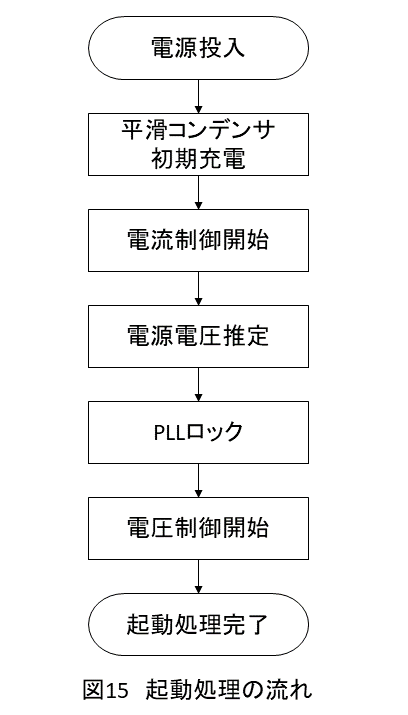
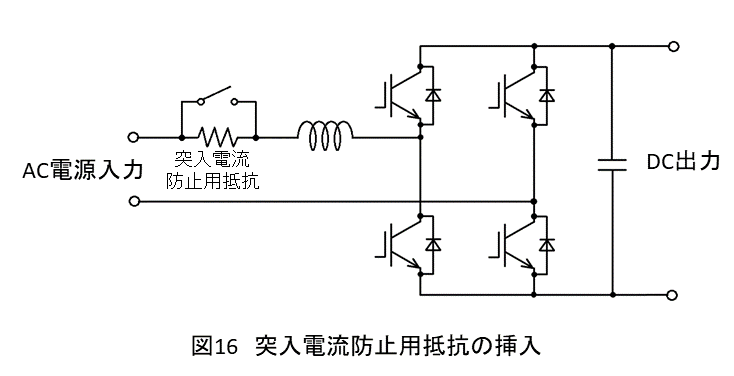
電源投入前は平滑コンデンサの電荷はゼロであり，この状態で直接的に電源を接続すると，平滑コンデンサを急速に充電するため瞬間的に大きな突入電流が流れます．突入電流は電源スイッチやブレーカーの接点を溶着させたり，スイッチング素子中の還流ダイオードを破壊したりする恐れがあります．突入電流を防止するためには，図16のように電源ラインにある程度の抵抗を介して平滑コンデンサをゆっくり初期充電させる必要があります．一定時間が経過し，平滑コンデンサが所定の電圧に達した所でその抵抗を短絡し，初期充電を完了させます．なお，平滑コンデンサの充電が完了するまではPWMコンバータの制御はできないため，スイッチング素子は駆動せず全てオフとし，還流ダイオードのみ導通させます．

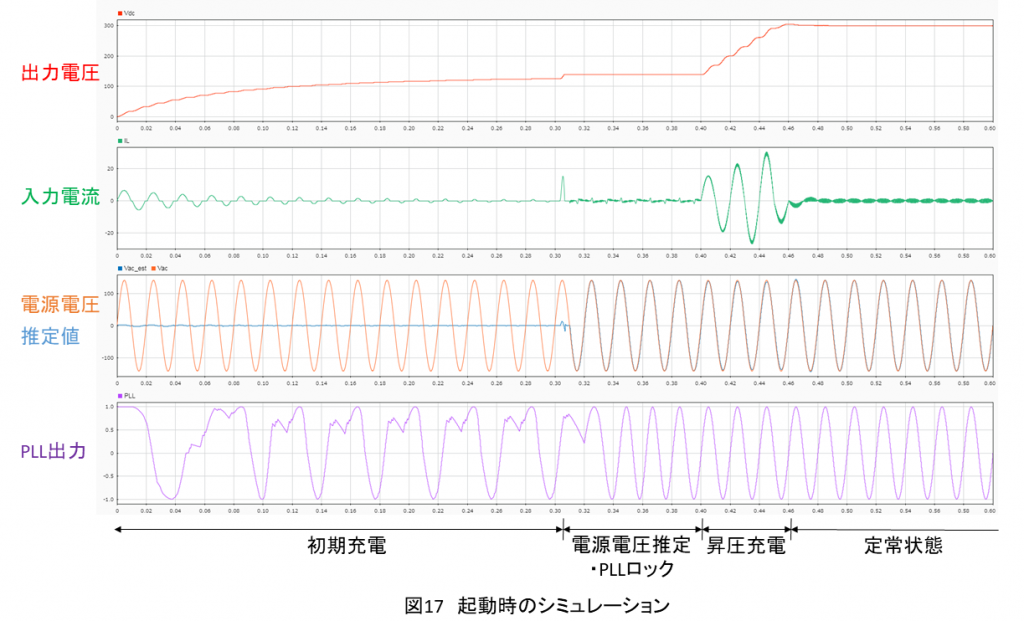
平滑コンデンサの初期充電が完了したら，PWMコンバータの電流制御を開始します．電源電圧センサレスの場合，この時点では電源電圧の位相角の検出ができていないため，電圧制御器は動作させず，電流制御の指令値はゼロとしておきます．この間に，電源電圧オブザーバにより電源電圧の推定を行い，それに従ってPLLにより電源電圧の位相角を取得します．一定時間経過した後，電源電圧オブザーバとPLLが定常状態となってから，電圧制御を開始して昇圧により平滑コンデンサを所望の出力電圧となるまで充電します．電圧制御が定常状態となり，これにてPWMコンバータの起動処理が完了します．
PWMコンバータの起動時のシミュレーション例を図17に示します．

8. 制御プログラムの構成

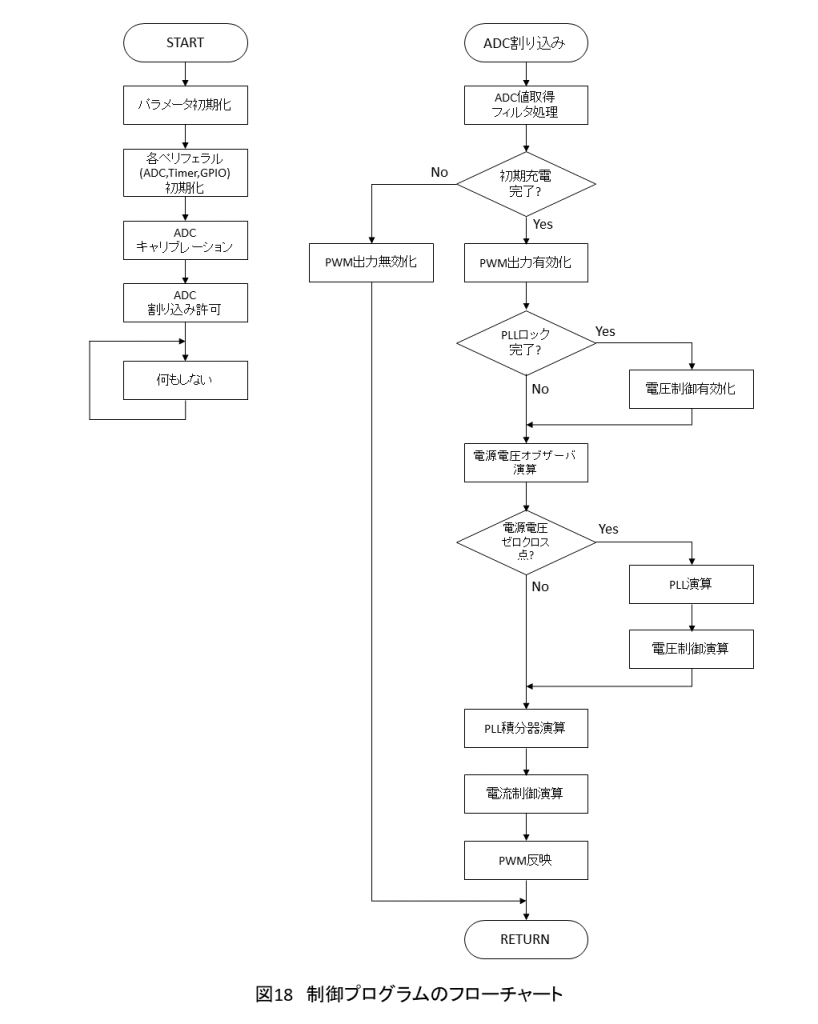
制御プログラムのフローチャートを図18に示します．メインプログラムでは各初期化や設定を行った後，何もしないループにより割り込みの待機を行います．入力電流と出力電圧を取得するA/Dコンバータ(ADC)をPWMに同期させて動作させ，変換が終了した時に割り込みを発生させます．ADC割り込みプログラムではADCから取得した値をもとに各制御演算を実行します．なお，出力電圧にデッドビート制御を適用する場合，ノイズの影響が大きくなりやすいため，出力電圧に対してLPFによるフィルタ処理を設けます．突入電流防止回路による初期充電が完了したかを，出力電圧あるいは時間経過により判断し，それに応じてPWMの出力を有効化します．電源電圧オブザーバ，PLL，電流制御器の動作を開始し，一定時間経過してPLLの位相角が電源と一致したら電圧制御器も有効化させます．電源電圧オブザーバから電源電圧のゼロクロス点を検出し，そのときだけPLL制御と電圧制御器の演算を行います．

9. 製作

製作したPWMコンバータを搭載する三相インバータの概観を図19に示します．PWMコンバータの仕様として，スイッチング周波数は18kHz，出力電圧は300Vで設定しました．

ヒートシンクにはインバータとコンバータそれぞれのIGBTモジュールを取り付け，ブリッジ回路を構成しています．バスバーを用いて平滑用の電解コンデンサとできるだけ短くなるように配線します．IGBTのブリッジ回路部分を図20に示します．緑色の部品はスナバ用のフィルムコンデンサです．

突入電流防止回路周りを図21に示します．突入電流防止用抵抗をバイパスする電磁開閉器をタイマーリレーにより駆動するような構成となっています．電磁開閉器がオンされると，マイコンにより初期充電後の処理が開始されます．

制御回路基板とDC-DCコンバータ基板を図22に示します．制御回路基板に乗っている2つのQFPパッケージのICは，それぞれPWMコンバータとインバータの制御用マイコンであり，PWMコンバータにはSTM32F303K8T6，インバータにはSTM32F405RGT6を使用しています．制御回路基板の上側部分は電流・電圧検出用の絶縁アンプと絶縁DC-DCコンバータで，右側部分はIGBTのゲートドライブ回路です．また，DC-DCコンバータ基板は，PWMコンバータの出力であるDCリンク電圧から制御回路とタイマーリレーの電源用の電圧に変換する，自励式フライバックコンバータ(リンギングチョークコンバータ)を構成しています．

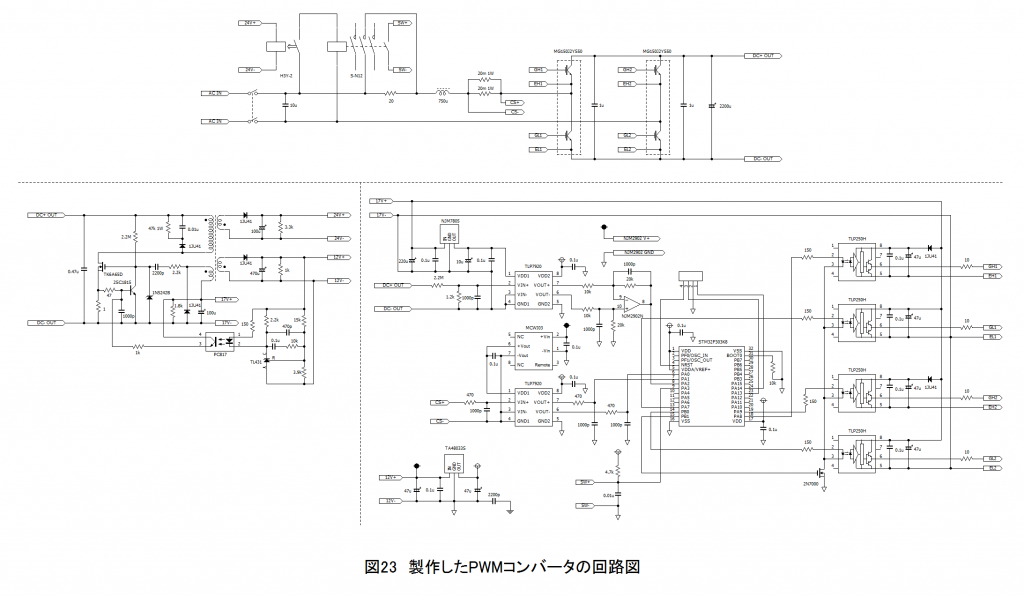
PWMコンバータに関与する部分のみの回路図を図23に示します．

制御マイコン(STM32F303K8T6)のソースコードはこちらに公開しておきます．

10. 動作確認

350W程の負荷を与えたときの電源電圧，電力，力率の計測値を図24に示します．高力率で動作できていることがわかります．

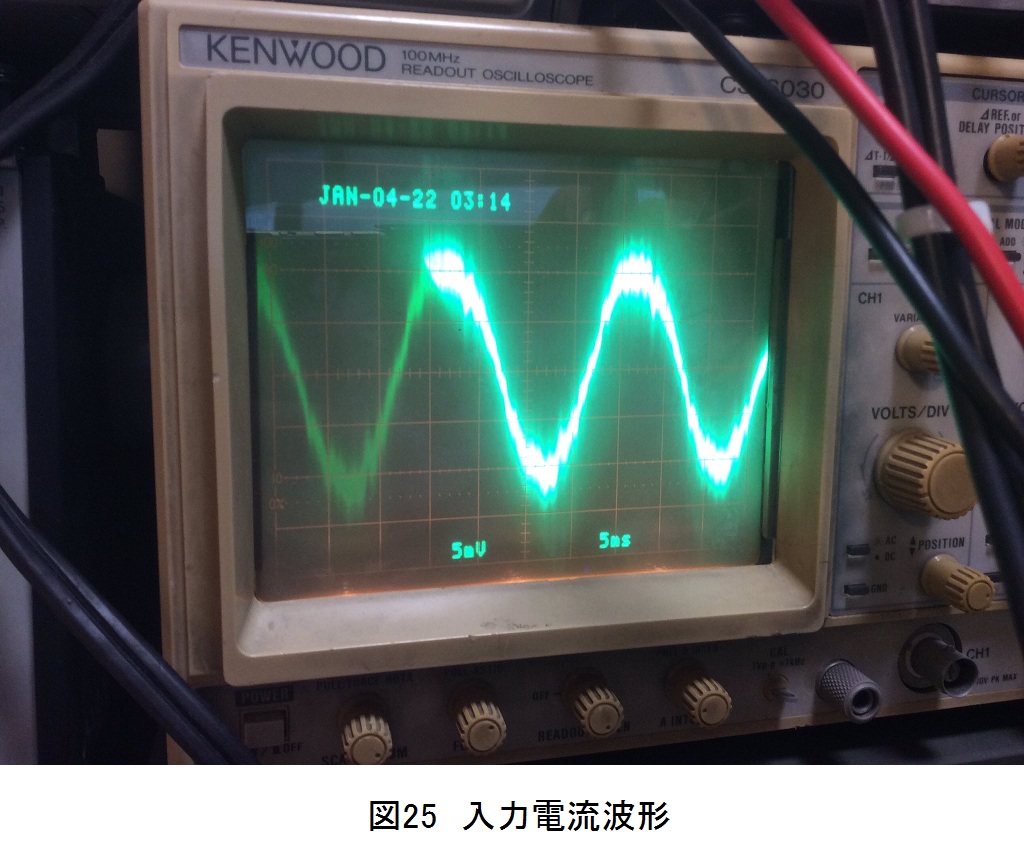
入力電流波形を図25に示します．正弦波状の電流となるように制御できています．

負荷を変動させているときの出力電圧の様子です．次の動画のように，300Vに一定制御されていることがわかります．

約700Wの負荷をステップ状に与えた時のDCリンク電圧の応答、殆ど振れてません pic.twitter.com/NMDjTCX7QX

— タマゴさん (@86723nasogamat) January 3, 2022

電源投入時の入力電流波形の様子を次の動画に示します．

負荷繋いだままでのPWMコンバータ始動時の入力電流の遷移がエモい pic.twitter.com/Vqlu21qLme

— タマゴさん (@86723nasogamat) January 18, 2022

DCリンク側から逆方向に電力を入力し，系統連系インバータとして回生動作させている様子を次の動画に示します．電源電圧に対して入力電流の位相が反転しており，電力を電源側に回生していることがわかります．

PWMコンバータ↔︎系統連系インバータ pic.twitter.com/CLB0HyQQEN

— タマゴさん (@86723nasogamat) January 18, 2022

11. まとめ

単相PWMコンバータについて，制御系の構成方法を主軸として紹介しました．また，その制御系を利用して実際にPWMコンバータを製作し，有効に動作することを確認しました．ここで述べた制御方法や回路構成は独自性が多いため，あくまで一例として捉えて頂けると幸いです．