幼女でもわかる状態平均化法 スイッチングコンバータの伝達関数モデル化

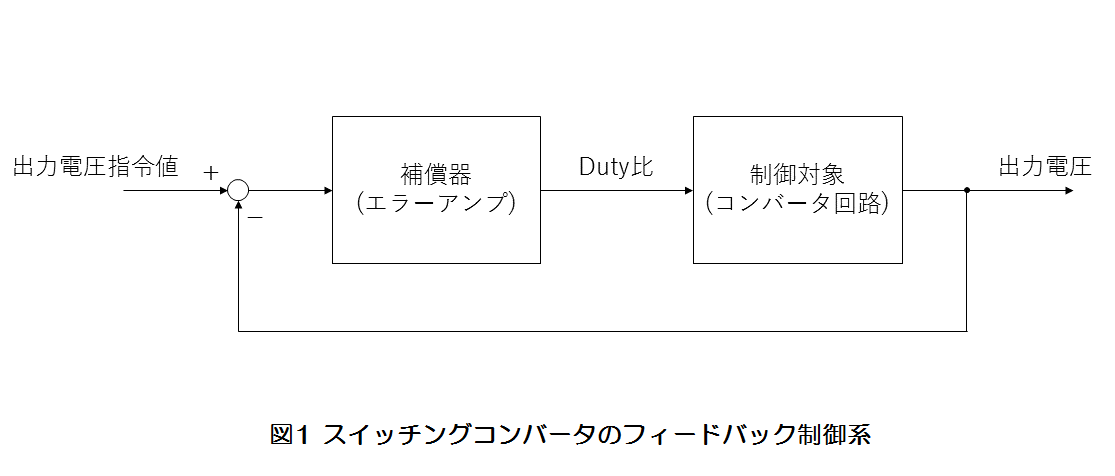
一般的にスイッチングコンバータは出力電圧を一定に保つため、図1に示すようにフィードバック制御によりスイッチの通流率(Duty比)を操作する必要があります。安定性や応答性が優れたフィードバック制御系を構成するためには、適切なパラメータの補償器を設計する必要があり、制御対象であるスイッチングコンバータのモデルが必要となります。スイッチングコンバータのモデルを得る方法として、実際に回路を組んで計測器を用いて周波数応答を測定する、回路シミュレータを用いるなどが考えられますが、それらにはそれ相応の環境や手間が必要だったり、素子定数を変更する度に実験を繰り返すことになったりするのであまり好ましくありません。制御対象を伝達関数などの数式モデルとして表現することができれば、素子定数をそれに代入するだけで特性を確認しやすくなり、モデルの扱いが比較的容易となります。ここでは、スイッチングコンバータを数式モデル化するためによく使われる、状態平均化法という解析手法を紹介していきます。

必要な数学的知識：大学初等レベル (行列、全微分、ラプラス変換など)

状態平均化法の概要

スイッチングコンバータはインダクタ電流が連続モードである場合、スイッチのON・OFFに応じた2種類の異なる電気回路が交互に切り替わるような動作をします。昇圧コンバータを例とすると、図2のように等価回路の構成が切り替わることがわかります。

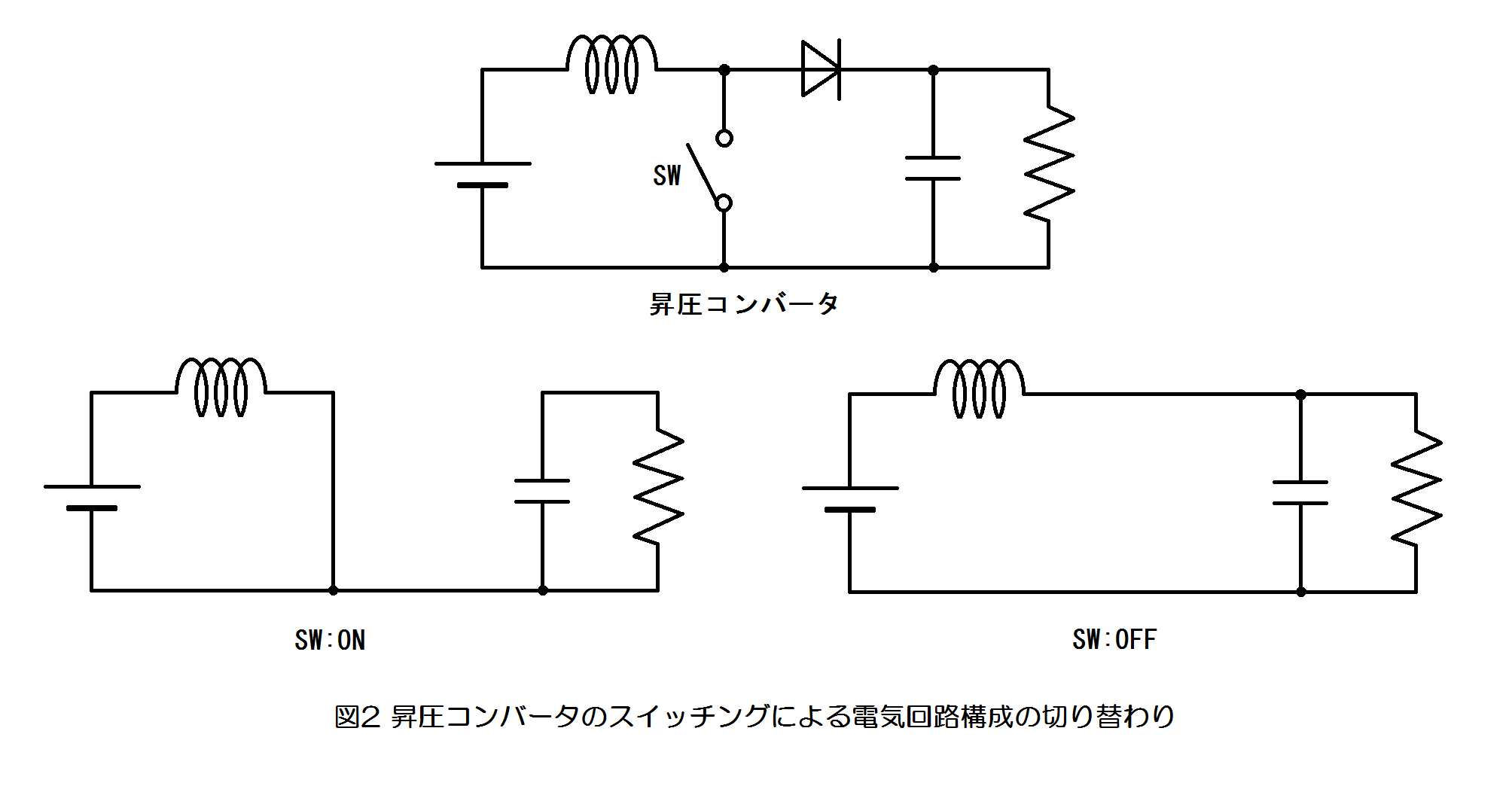
2種類それぞれのスイッチング状態の回路を単体でみたときは受動線形素子のみの電気回路であり、線形システムとして容易に解析が可能ですが、定常的にこれらが高周波数で切り替わるとなると非線形システムとなり、解析が困難となります。そこで、これら2種類の回路の状態空間モデルを切り替わりの比率、すなわちDuty比で重み付けして平均化し、線形システムに近似させて解析する、状態平均化法という手法が使われます。状態空間モデルとは(1)式のような1階の連立微分方程式(状態方程式)と(2)式の出力方程式で表される数式モデルです。ここでは入力変数、は状態変数(状態ベクトル)、は出力変数です。入力変数や出力変数をベクトルとし、多入力多出力のシステムを表現することも可能です。, , は係数行列、係数ベクトルです。
$$\frac{d\boldsymbol{x}}{dt}=\boldsymbol{Ax}+\boldsymbol{b}u\tag{1}$$$$y=\boldsymbol{cx}\tag{2}$$
電気回路を状態空間モデルで表現する場合、基本的にコンデンサ電圧とインダクタ電流を状態変数として扱います。また、状態平均化法によるコンバータの解析では入力変数を入力電圧とし、出力変数を出力電圧または状態変数であるコンデンサ電圧とインダクタ電流とします。コンデンサ電圧とインダクタ電流の状態変数をそのまま出力変数とする場合は状態方程式のみを扱えば良いですが、コンデンサの等価直列抵抗(ESR)を考慮してモデル化する場合は出力電圧がコンデンサ電圧とは別の値となるため、出力方程式も立式し扱う必要があります。

図2の昇圧コンバータを解析するために必要な変数を加えると図3のようになります。

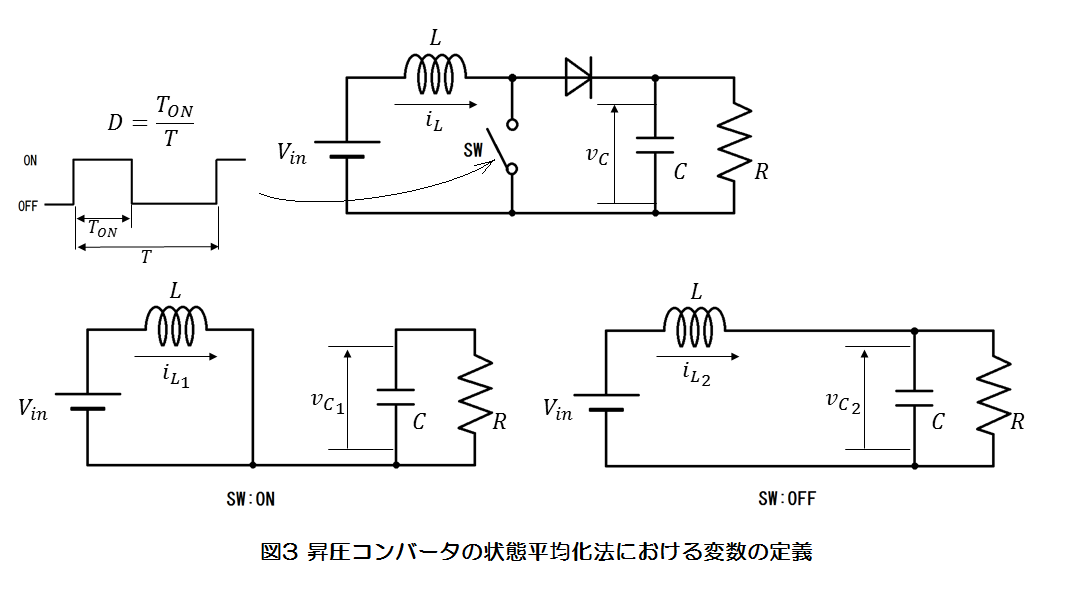
まず、それぞれのスイッチング状態での回路についての状態方程式を(3)式、(4)式のように立てます。, とすると、(3)式はSWがONのとき、(4)式はOFFのときの状態方程式となります。
$$\frac{d\boldsymbol{x_1}}{dt}=\boldsymbol{A_1}\boldsymbol{x_1}+\boldsymbol{b_1}V_{in}\tag{3}$$$$\frac{d\boldsymbol{x_2}}{dt}=\boldsymbol{A_2}\boldsymbol{x_2}+\boldsymbol{b_2}V_{in}\tag{4}$$
これらをDuty比で重み付けし、それぞれの平均をとるような操作をすると(5)式となります。ただし、であり、インダクタ電流、コンデンサ電圧のスイッチングによる高周波リプルを除去し平均化したような値の状態変数です。
$$\frac{d\boldsymbol{\overline{x}}}{dt}= \{ D\boldsymbol{A_1}+(1-D)\boldsymbol{A_2} \} \boldsymbol{\overline{x}}+ \{ D\boldsymbol{b_1}+(1-D)\boldsymbol{b_2} \}V_{in}\tag{5}$$
この(5)式を状態平均化方程式といい、状態平均化法ではこれを立式し、特性解析や伝達関数モデル化を行います。

状態平均化方程式の導出

昇圧コンバータを例として、実際に係数行列と係数ベクトルを求め状態平均化方程式を導出してみましょう。より正確にモデル化するためには各素子の寄生抵抗も考慮し解析を行う必要がありますが、ここでは簡潔にするため寄生抵抗を無視し理想的なコンバータ回路として解析していきます。

まず、図4に示すような昇圧コンバータのスイッチがONのときの状態方程式を求めます。

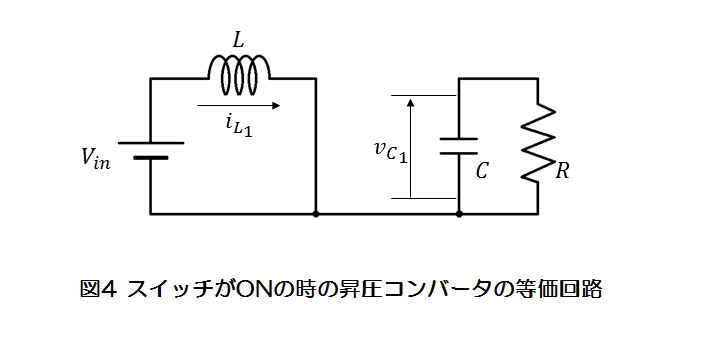
インダクタの電圧についての関係は(6)式のようになります。
$$L\frac{d{{i_L}_1}}{dt}=V_{in}\tag{6}$$
状態方程式の形にするため、(7)式のように変形し、左辺を微分演算のみにしておきます。
$$\frac{d{{i_L}_1}}{dt}=\frac{1}{L}V_{in}\tag{7}$$
また、コンデンサの電流についての関係を求め左辺を微分演算のみにすると(8)式のようになります。
$$\frac{d{{v_C}_1}}{dt}=-\frac{1}{CR}{v_C}_1\tag{8}$$
(7)式、(8)式より、行列形式で表記した状態方程式は(9)式になります。
$$\frac{d}{dt}\left[\begin{array}{c}{i_L}_1 \\ {v_C}_1 \end{array}\right]=\left[\begin{array}{cc}0 & 0 \\ 0 & -\frac{1}{CR} \end{array}\right]\left[\begin{array}{c}{i_L}_1 \\ {v_C}_1 \end{array}\right]+\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right]V_{in}\tag{9}$$
とすると(9)式は(10)式となります。
$$\frac{d\boldsymbol{x_1}}{dt}=\left[\begin{array}{cc}0 & 0 \\ 0 & -\frac{1}{CR} \end{array}\right]\boldsymbol{x_1}+\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right]V_{in}\tag{10}$$
これでスイッチがONのときの昇圧コンバータの状態方程式が求まりました。次いでスイッチがOFFのときも求めていきます。
図5に昇圧コンバータのスイッチがOFFのときの等価回路を示します。

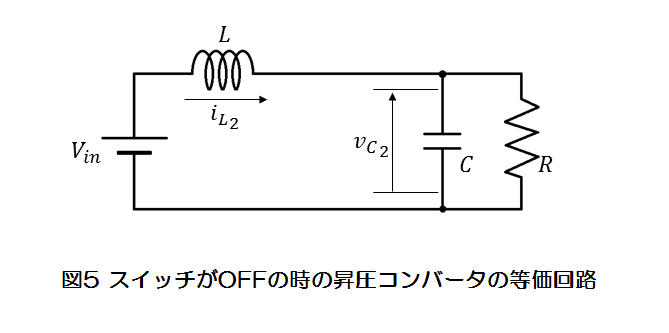
インダクタの電圧についての関係は(11)式となります。
$$\frac{d{{i_L}_2}}{dt}=-\frac{1}{L}{{v_C}_2}+\frac{1}{L}V_{in}\tag{11}$$
また、コンデンサの電流についての関係は(12)式となります。
$$\frac{d{{v_C}_2}}{dt}=\frac{1}{C}{{i_L}_2}-\frac{1}{CR}{v_C}_2\tag{12}$$
とし、(11)式、(12)式より、状態方程式は(13)式となります。
$$\frac{d\boldsymbol{x_2}}{dt}=\left[\begin{array}{cc}0 & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{CR}\end{array}\right]\boldsymbol{x_2}+\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right]V_{in}\tag{13}$$
スイッチがON・OFF両方のときの状態方程式が求まったので、状態平均化方程式を求めます。状態変数をとし、(10)式と(13)式より、(5)式のようにDuty比で重み付き平均をとると(14)式のようになります。

$$\frac{d\boldsymbol{\overline{x}}}{dt}=\left \{ D\left[\begin{array}{cc}0 & 0 \\ 0 & -\frac{1}{CR} \end{array}\right]+(1-D)\left[\begin{array}{cc}0 & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{CR} \end{array}\right] \right \} \boldsymbol{\overline{x}}+ \left \{ D\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right]+(1-D)\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right] \right  \}V_{in}\tag{14}$$
(14)式を計算し整理すると(15)式となり、これが昇圧コンバータの状態平均化方程式となります。
$$\frac{d\boldsymbol{\overline{x}}}{dt}=\left[\begin{array}{cc}0 & -\frac{1-D}{L} \\ \frac{1-D}{C} & -\frac{1}{CR} \end{array}\right]\boldsymbol{\overline{x}}+\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right]V_{in}\tag{15}$$
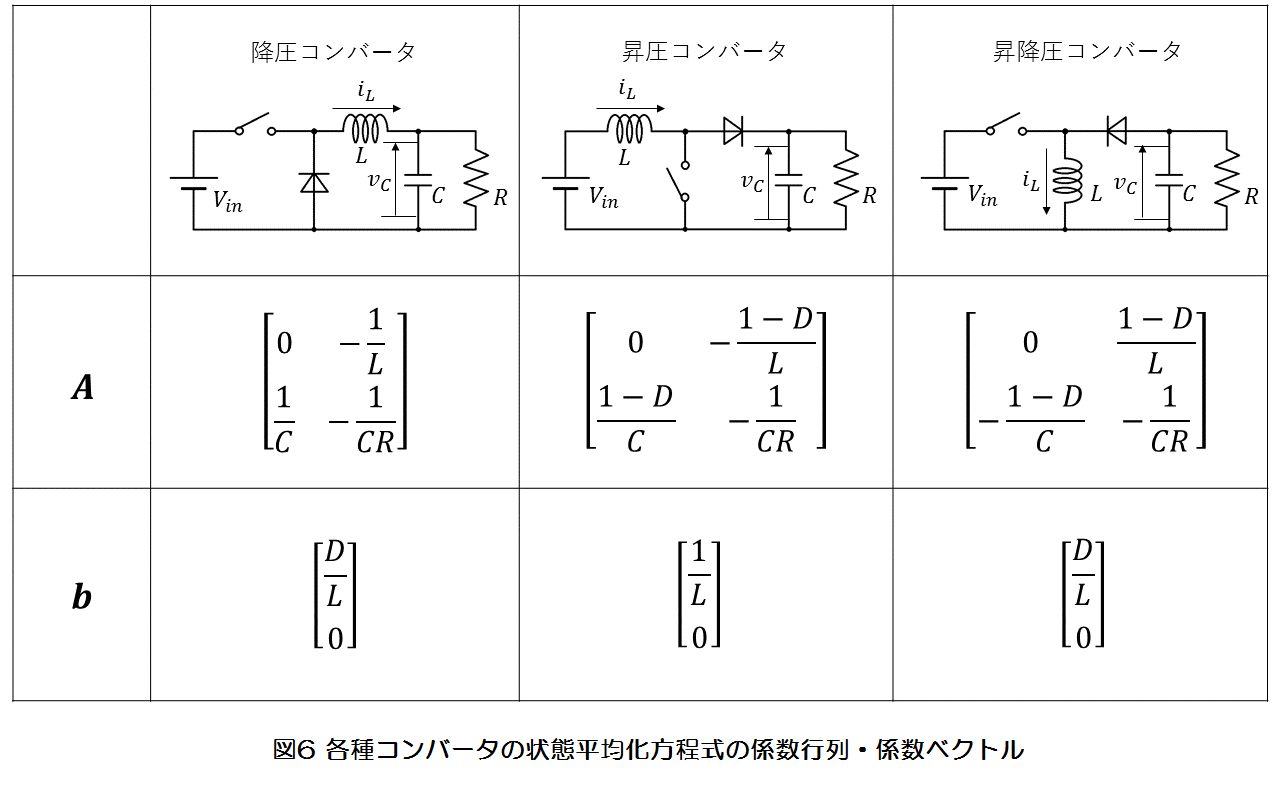
降圧コンバータ、昇降圧コンバータの状態平均化方程式も同様に求めることができます。状態平均化方程式を一般的に(16)式とし、各種のコンバータの, を図6に示します。
$$\frac{d\boldsymbol{\overline{x}}}{dt}=\boldsymbol{A} \boldsymbol{\overline{x}}+\boldsymbol{b}V_{in}\tag{16}$$

静特性

状態変数が時間に伴って変化せず常に一定、すなわち定常状態での特性を静特性といいます。コンバータが定常状態で動作している場合、状態変数を時間微分した値はゼロとなります。つまり、状態平均化方程式を用いると定常状態では(17)式が成り立ちます。
$$\frac{d\boldsymbol{\overline{x}}}{dt}=\boldsymbol{A} \boldsymbol{\overline{x}}+\boldsymbol{b}V_{in}=\left[\begin{array}{c}0 \\ 0 \end{array}\right]\tag{17}$$
先に求めた昇圧コンバータの状態平均化方程式を用いて静特性を見てみましょう。(15)式より定常状態の状態平均化方程式は(18)式となります。
$$\left[\begin{array}{cc}0 & -\frac{1-D}{L} \\ \frac{1-D}{C} & -\frac{1}{CR} \end{array}\right]\boldsymbol{\overline{x}}+\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right]V_{in}=\left[\begin{array}{c}0 \\ 0 \end{array}\right]\tag{18}$$
このときの状態変数について解くと、(19)式のようになります。
$$\begin{align}\boldsymbol{\overline{x}}&=-\left[\begin{array}{cc}0 & -\frac{1-D}{L} \\ \frac{1-D}{C} & -\frac{1}{CR} \end{array}\right]^{-1} \left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right]V_{in} \\ &=-\frac{LC}{(1-D)^2} \left[\begin{array}{cc}-\frac{1}{CR} & \frac{1-D}{L} \\ -\frac{1-D}{C} & 0 \end{array}\right]\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right]V_{in} \\ &=-\frac{LC}{(1-D)^2} \left[\begin{array}{c}-\frac{1}{LCR} \\ -\frac{1-D}{LC} \end{array}\right]V_{in} \\ &=\left[\begin{array}{c}\frac{1}{(1-D)^2R} \\ \frac{1}{1-D} \end{array}\right]V_{in}\end{align}\tag{19}$$
したがって、入力電圧とインダクタ電流、コンデンサ電圧の関係は(20)式、(21)式のようになることがわかります。
$$\overline{i_L}=\frac{1}{(1-D)^2R}V_{in}\tag{20}$$$$\overline{v_C}=\frac{1}{1-D}V_{in}\tag{21}$$
(21)式の昇圧コンバータの入出力電圧の関係式は公式としてご存知の方が多いでしょう。このように状態平均化法により導出することができます。
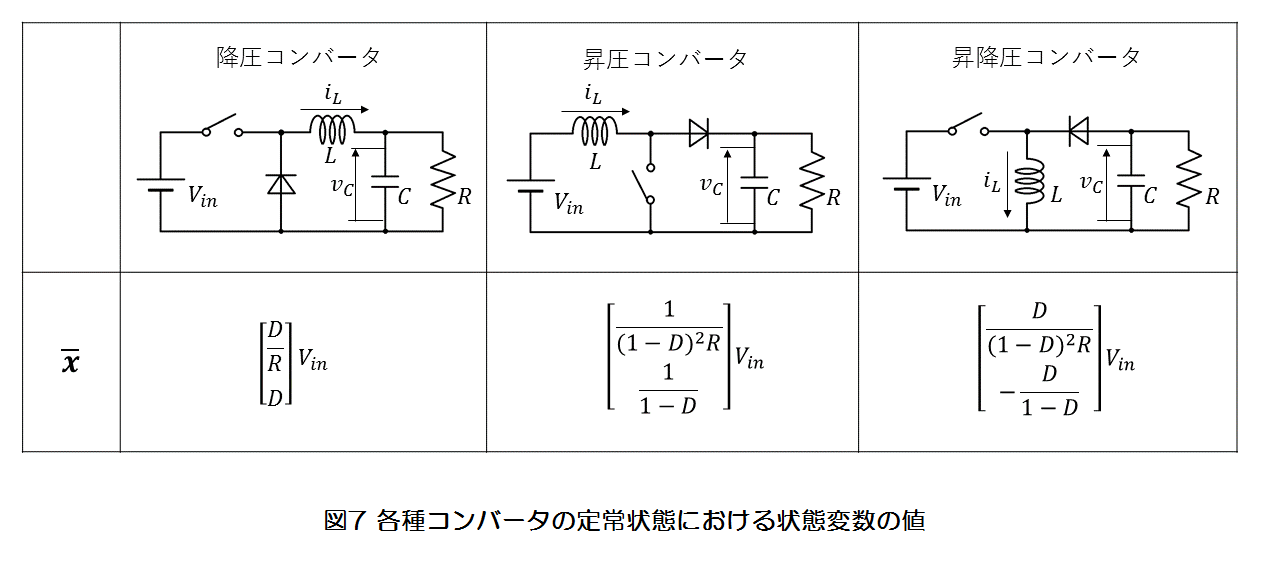
各種コンバータの静特性を図7に示します。

動特性(伝達関数)

定常状態に対して、入力としてあるパラメータが微小変化したときの状態変数や出力変数の応答特性を動特性といいます。コンバータの解析で微小変化させるパラメータはDuty比、負荷抵抗、入力電圧とし、それぞれを入力としたときの伝達関数を求めていきます。特にDuty比を入力とする伝達関数は制御系を設計する上で必要不可欠であり、最も重要な特性となります。状態変数のうちコンデンサ電圧を出力とする伝達関数は、出力電圧を制御するための制御系として必要であるのは勿論のこと、インダクタ電流を出力とする伝達関数は、電流モード制御を構成する際に必要となります。また、負荷抵抗(出力電流)の変動に対する出力電圧の応答をロードレギュレーション、入力電圧の変動に対する応答をラインレギュレーションといい、コンバータの性能評価において重要な特性です。
各パラメータの微小変化を意味する記号としてを用い、状態平均化方程式の各パラメータを以下のように置き換えます。
$$D\rightarrow D+\mathit{\Delta}D \\ R\rightarrow R+\mathit{\Delta}R \\ V_{in}\rightarrow V_{in}+\mathit{\Delta}V_{in}$$$$\overline{i_L}\rightarrow \overline{i_L}+\mathit{\Delta}\overline{i_L} \\ \overline{v_C}\rightarrow \overline{v_C}+\mathit{\Delta}\overline{v_C}$$
これらに伴い、(16)式のような一般形の状態平均化方程式の各パラメータは以下のように置き換わります。
$$\boldsymbol{A}\rightarrow \boldsymbol{A}+\mathit{\Delta}\boldsymbol{A} \\ \boldsymbol{b}\rightarrow \boldsymbol{b}+\mathit{\Delta}\boldsymbol{b}$$$$\boldsymbol{\overline{x}}\rightarrow \boldsymbol{\overline{x}}+\mathit{\Delta}\boldsymbol{\overline{x}}$$
したがって、(16)式より(22)式が成り立ちます。
$$\frac{d(\boldsymbol{\overline{x}}+\mathit{\Delta}\boldsymbol{\overline{x}})}{dt}=(\boldsymbol{A}+\mathit{\Delta}\boldsymbol{A}) (\boldsymbol{\overline{x}}+\mathit{\Delta}\boldsymbol{\overline{x}})+(\boldsymbol{b}+\mathit{\Delta}\boldsymbol{b}) (V_{in}+\mathit{\Delta}V_{in})\tag{22}$$
これを展開すると(23)式となります。
$$\frac{d\boldsymbol{\overline{x}}}{dt}+\frac{d\mathit{\Delta}\boldsymbol{\overline{x}}}{dt}=\boldsymbol{A}\boldsymbol{\overline{x}}+\boldsymbol{A}\mathit{\Delta}\boldsymbol{\overline{x}}+\mathit{\Delta}\boldsymbol{A}\boldsymbol{\overline{x}}+\mathit{\Delta}\boldsymbol{A}\mathit{\Delta}\boldsymbol{\overline{x}}+\boldsymbol{b}V_{in}+\mathit{\Delta}\boldsymbol{b}V_{in}+\boldsymbol{b}\mathit{\Delta}V_{in}+\mathit{\Delta}\boldsymbol{b}\mathit{\Delta}V_{in}\tag{23}$$
ここで、, というような2次の微小項をゼロとみなし消去すると(24)式となります。
$$\frac{d\boldsymbol{\overline{x}}}{dt}+\frac{d\mathit{\Delta}\boldsymbol{\overline{x}}}{dt}=\boldsymbol{A}\boldsymbol{\overline{x}}+\boldsymbol{b}V_{in}+\boldsymbol{A}\mathit{\Delta}\boldsymbol{\overline{x}}+\mathit{\Delta}\boldsymbol{A}\boldsymbol{\overline{x}}+\mathit{\Delta}\boldsymbol{b}V_{in}+\boldsymbol{b}\mathit{\Delta}V_{in}\tag{24}$$
(24)式において左辺1項目、右辺2項目までは定常状態での状態平均化方程式として成り立っている部分であるため、両辺からこれらを消去できます。したがって、(25)式となります。
$$\frac{d\mathit{\Delta}\boldsymbol{\overline{x}}}{dt}=\boldsymbol{A}\mathit{\Delta}\boldsymbol{\overline{x}}+\mathit{\Delta}\boldsymbol{A}\boldsymbol{\overline{x}}+\mathit{\Delta}\boldsymbol{b}V_{in}+\boldsymbol{b}\mathit{\Delta}V_{in}\tag{25}$$
は, の関数、はを含むことは無いためのみの関数であるとし、それぞれ(26)式、(27)式のように全微分します。(は一般的に微小変化量を示す記号と扱いは同じです。)
$$\mathit{\Delta}\boldsymbol{A}=\frac{\partial \boldsymbol{A}}{\partial D}\mathit{\Delta}D+\frac{\partial \boldsymbol{A}}{\partial R}\mathit{\Delta}R\tag{26}$$$$\mathit{\Delta}\boldsymbol{b}=\frac{\partial \boldsymbol{b}}{\partial D}\mathit{\Delta}D\tag{27}$$
したがって(25)式、(26)式、(27)式より(28)式となります。
$$\frac{d\mathit{\Delta}\boldsymbol{\overline{x}}}{dt}=\boldsymbol{A}\mathit{\Delta}\boldsymbol{\overline{x}}+\left(\frac{\partial \boldsymbol{A}}{\partial D}\mathit{\Delta}D+\frac{\partial \boldsymbol{A}}{\partial R}\mathit{\Delta}R\right)\boldsymbol{\overline{x}}+\frac{\partial \boldsymbol{b}}{\partial D}\mathit{\Delta}DV_{in}+\boldsymbol{b}\mathit{\Delta}V_{in}\tag{28}$$
(28)式をラプラス変換すると(29)式となります。ここで各微小変化分のパラメータは時間関数からsの関数となります。は状態ベクトルと同次の単位行列です。
$$s\boldsymbol{I}\mathit{\Delta}\boldsymbol{\overline{x}}(s)=\boldsymbol{A}\mathit{\Delta}\boldsymbol{\overline{x}}(s)+\left\{\frac{\partial \boldsymbol{A}}{\partial D}\mathit{\Delta}D(s)+\frac{\partial \boldsymbol{A}}{\partial R}\mathit{\Delta}R(s)\right\}\boldsymbol{\overline{x}}+\frac{\partial \boldsymbol{b}}{\partial D}\mathit{\Delta}D(s)V_{in}+\boldsymbol{b}\mathit{\Delta}V_{in}(s)\tag{29}$$
(29)式より(30)式が成り立ちます。
$$\begin{align}\mathit{\Delta}\boldsymbol{\overline{x}}(s)&=(s\boldsymbol{I}-\boldsymbol{A})^{-1}\left[\left\{\frac{\partial \boldsymbol{A}}{\partial D}\mathit{\Delta}D(s)+\frac{\partial \boldsymbol{A}}{\partial R}\mathit{\Delta}R(s)\right\}\boldsymbol{\overline{x}}+\frac{\partial \boldsymbol{b}}{\partial D}\mathit{\Delta}D(s)V_{in}+\boldsymbol{b}\mathit{\Delta}V_{in}(s)\right] \\ &=(s\boldsymbol{I}-\boldsymbol{A})^{-1}\left[\left(\frac{\partial \boldsymbol{A}}{\partial D}\boldsymbol{\overline{x}}+\frac{\partial \boldsymbol{b}}{\partial D}V_{in}\right)\mathit{\Delta}D(s)+\frac{\partial \boldsymbol{A}}{\partial R}\boldsymbol{\overline{x}}\mathit{\Delta}R(s)+\boldsymbol{b}\mathit{\Delta}V_{in}(s)\right]\end{align}\tag{30}$$
(30)式より、, , を入力とし、を出力とした伝達関数が(31)式、(32)式、(33)式のように求まります。
$$\begin{align}\frac{\mathit{\Delta}\boldsymbol{\overline{x}}(s)}{\mathit{\Delta}D(s)}&=(s\boldsymbol{I}-\boldsymbol{A})^{-1}\left(\frac{\partial \boldsymbol{A}}{\partial D}\boldsymbol{\overline{x}}+\frac{\partial \boldsymbol{b}}{\partial D}V_{in}\right)\tag{31} \\ \frac{\mathit{\Delta}\boldsymbol{\overline{x}}(s)}{\mathit{\Delta}R(s)}&=(s\boldsymbol{I}-\boldsymbol{A})^{-1}\frac{\partial \boldsymbol{A}}{\partial R}\boldsymbol{\overline{x}}\tag{32} \\ \frac{\mathit{\Delta}\boldsymbol{\overline{x}}(s)}{\mathit{\Delta}V_{in}(s)}&=(s\boldsymbol{I}-\boldsymbol{A})^{-1}\boldsymbol{b}\tag{33}\end{align}$$
実際に昇圧コンバータの状態平均化方程式の係数を代入して伝達関数を求めてみましょう。まず、を計算すると(34)式のようになります。
$$\begin{align}(s\boldsymbol{I}-\boldsymbol{A})^{-1}&=\left(\left[\begin{array}{cc}s & 0 \\ 0 & s \ \end{array}\right]-\left[\begin{array}{cc}0 & -\frac{1-D}{L} \\ \frac{1-D}{C} & -\frac{1}{CR} \end{array}\right]\right)^{-1}\\ &=\left[\begin{array}{cc}s & \frac{1-D}{L} \\ -\frac{1-D}{C} & s+\frac{1}{CR} \end{array}\right]^{-1} \\ &=\frac{1}{s\left(s+\frac{1}{CR}\right)+\frac{(1-D)^2}{LC}}\left[\begin{array}{cc}s+\frac{1}{CR} & -\frac{1-D}{L} \\ \frac{1-D}{C} & s \end{array}\right] \\ &=\frac{1}{LCs^2+\frac{L}{R}s+(1-D)^2}\left[\begin{array}{cc}LCs+\frac{L}{R} & -C(1-D) \\ L(1-D) & LCs \end{array}\right]\end{align}\tag{34}$$
よって、(31)式より(35)式となります。
$$\begin{align}\frac{\mathit{\Delta}\boldsymbol{\overline{x}}(s)}{\mathit{\Delta}D(s)}&=(s\boldsymbol{I}-\boldsymbol{A})^{-1}\left(\frac{\partial \boldsymbol{A}}{\partial D}\boldsymbol{\overline{x}}+\frac{\partial \boldsymbol{b}}{\partial D}V_{in}\right) \\  &=\frac{1}{LCs^2+\frac{L}{R}s+(1-D)^2}\left[\begin{array}{cc}LCs+\frac{L}{R} & -C(1-D) \\ L(1-D) & LCs \ \end{array}\right]\left(\frac{\partial}{\partial D}\left[\begin{array}{cc}0 & -\frac{1-D}{L} \\ \frac{1-D}{C} & -\frac{1}{CR} \end{array}\right]\boldsymbol{\overline{x}}+\frac{\partial}{\partial D}\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right]V_{in}\right)\\ &=\frac{1}{LCs^2+\frac{L}{R}s+(1-D)^2}\left[\begin{array}{cc}LCs+\frac{L}{R} & -C(1-D) \\ L(1-D) & LCs \end{array}\right]\left[\begin{array}{cc}0 & \frac{1}{L} \\ -\frac{1}{C} & 0 \end{array}\right]\left[\begin{array}{c}\overline{i_L} \\ \overline{v_C} \end{array}\right] \\ &=\frac{1}{LCs^2+\frac{L}{R}s+(1-D)^2}\left[\begin{array}{c}C\overline{v_C}s+(1-D)\overline{i_L}+\frac{\overline{v_C}}{R} \\ -L\overline{i_L}s+(1-D)\overline{v_C} \end{array}\right]\end{align}\tag{35}$$
(32)式より(36)式となります。
$$\begin{align}\frac{\mathit{\Delta}\boldsymbol{\overline{x}}(s)}{\mathit{\Delta}R(s)}&=(s\boldsymbol{I}-\boldsymbol{A})^{-1}\frac{\partial \boldsymbol{A}}{\partial R}\boldsymbol{\overline{x}} \\ &=\frac{1}{LCs^2+\frac{L}{R}s+(1-D)^2}\left[\begin{array}{cc}LCs+\frac{L}{R} & -C(1-D) \\ L(1-D) & LCs \end{array}\right]\frac{\partial}{\partial R}\left[\begin{array}{cc}0 & -\frac{1-D}{L} \\ \frac{1-D}{C} & -\frac{1}{CR} \end{array}\right]\boldsymbol{\overline{x}} \\ &=\frac{1}{LCs^2+\frac{L}{R}s+(1-D)^2}\left[\begin{array}{cc}LCs+\frac{L}{R} & -C(1-D) \\ L(1-D) & LCs \end{array}\right]\left[\begin{array}{cc}0 & 0 \\ 0 & \frac{1}{CR^2} \end{array}\right]\left[\begin{array}{c}\overline{i_L} \\ \overline{v_C} \end{array}\right] \\ &=\frac{1}{LCs^2+\frac{L}{R}s+(1-D)^2}\left[\begin{array}{c}-\frac{(1-D)\overline{v_C}}{R^2}\\ \frac{L\overline{v_C}}{R^2}s \ \end{array}\right]\end{align}\tag{36}$$
(33)式より(37)式となります。
$$\begin{align}\frac{\mathit{\Delta}\boldsymbol{\overline{x}}(s)}{\mathit{\Delta}V_{in}(s)}&=(s\boldsymbol{I}-\boldsymbol{A})^{-1}\boldsymbol{b} \\ &=\frac{1}{LCs^2+\frac{L}{R}s+(1-D)^2}\left[\begin{array}{cc}LCs+\frac{L}{R} & -C(1-D) \\ L(1-D) & LCs \end{array}\right]\left[\begin{array}{c}\frac{1}{L} \\ 0 \end{array}\right] \\ &=\frac{1}{LCs^2+\frac{L}{R}s+(1-D)^2}\left[\begin{array}{c}Cs+\frac{1}{R}\\ 1-D \end{array}\right] \end{align}\tag{37}$$
このように、昇圧コンバータの伝達関数を求めることができます。降圧コンバータや昇降圧コンバータも同様に求められ、図8に各種コンバータの伝達関数を示します。

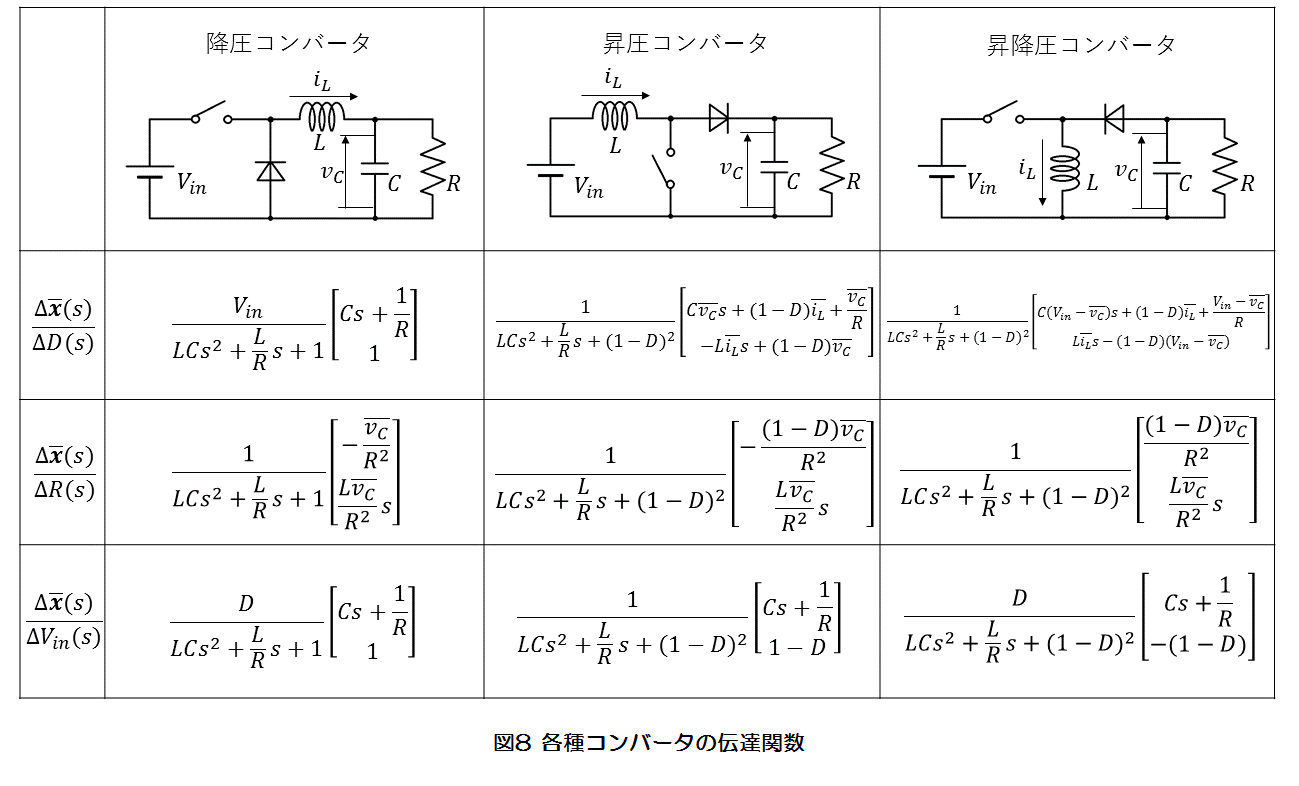
なお、図8における式は式(31)、式(32)、式(33)のみから求められるものを記しており、静特性の解析による定常状態での電圧や電流の関係を適用することで簡略化できる部分もあります。

昇圧コンバータの伝達関数の一例として、Duty比を入力、コンデンサ電圧を出力とする(38)式を取り上げ、その特性を見ていきましょう。
$$\frac{\mathit{\Delta}\overline{v_C}(s)}{\mathit{\Delta}D(s)}=\frac{ -L\overline{i_L}s+(1-D)\overline{v_C}}{LCs^2+\frac{L}{R}s+(1-D)^2}\tag{38}$$
分母に注目すると、2次遅れ要素を持っていることがわかり、(38)式のを掛けた分母と、固有角周波数、減衰係数とした2次遅れ要素の標準形の分母を(39)式のように比較します。
$$s^2+\frac{1}{CR}s+\frac{(1-D)^2}{LC}=s^2+2\zeta{\omega}_ns+{\omega}_n^2\tag{39}$$
(39)式より、減衰係数は(40)式、固有角周波数は(41)式となります。
$$\zeta=\frac{1}{2(1-D)R}\sqrt{\frac{L}{C}}\tag{40}$$$${\omega}_n=\frac{1-D}{\sqrt{LC}}\tag{41}$$
また(38)式の分子に注目すると、sの一次式であり零点を1つ持つことがわかります。(42)式を立て零点を求めると(43)式となります。
$$-L\overline{i_L}z+(1-D)\overline{v_C}=0\tag{42}$$$$z=\frac{(1-D)\overline{v_C}}{L\overline{i_L}}\tag{43}$$
この零点は常に正の値をとるので、不安定零点となります。不安定零点を有するシステムは、ステップ応答に対してアンダーシュートを生じるような非最小位相系であり、また周波数応答においてゲインを降下させずに位相を遅らせる働きをします。このため制御系が不安定になりやすく、高速な応答を得られるような設計が難しいということになります。昇降圧コンバータでも同様に不安定零点を有します。

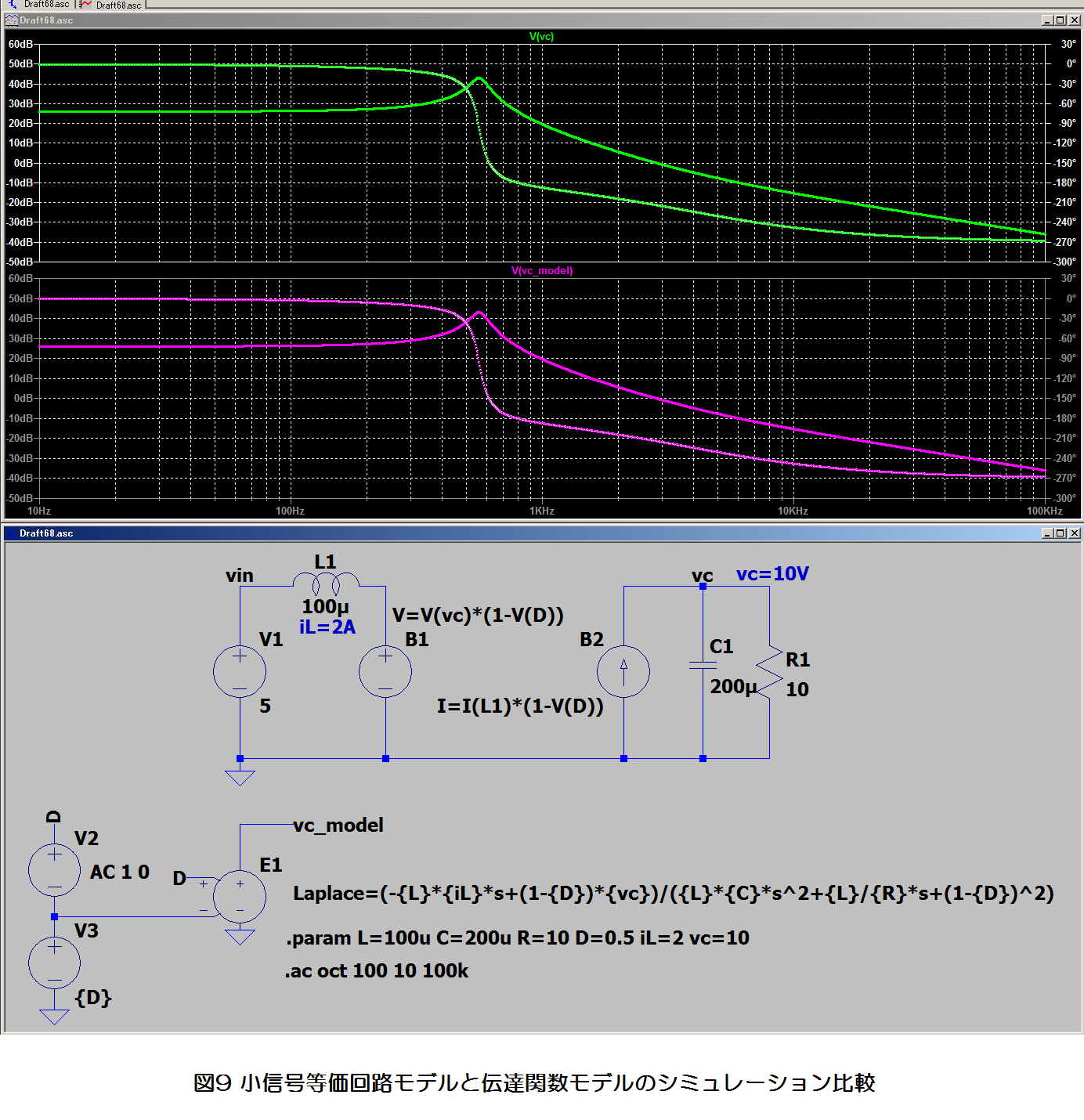
回路シミュレータを用いて適当なパラメータを設定し、伝達関数が正しくモデル化されているかを確認してみます。各パラメータを等しく設定した昇圧コンバータの小信号等価回路モデルと伝達関数モデルを用意し、それぞれの周波数応答を比較します。図9にそのシミュレーション結果を示します。上側のグラフが小信号等価回路モデル、下側のグラフが伝達関数モデルのボード線図であり、それぞれ殆ど一致していることがわかります。

インダクタ電流不連続モードについて

ここまで述べてきた解析方法はコンバータのインダクタ電流が連続モードであるという条件についてであり、不連続モードでは各特性が全く異なったものとなります。電流不連続モードの場合でも状態平均化法による解析が可能です。電流連続モードではスイッチングにより切り替わる等価回路の構成として、スイッチがONでダイオードがOFFの状態、スイッチがOFFでダイオードがONの状態という2種類がありました。電流不連続モードでは、それらに加えてスイッチとダイオードどちらもOFFの状態が存在するので、計3種類の回路の状態方程式を立てて平均化し、状態平均化方程式を立式することになります。しかし、その過程でインダクタ電流について平均化範囲を考慮する必要があり少々難しくなります。そのため、連続量となる状態変数の微分値となるような補助変数を導入することで、選択的に平均化したいパラメータを決めてから解析するような拡張状態平均化法というものがあり、これを用いてインダクタ電流は平均化せずに解析するというような手法もあります。
電流連続モードでの伝達関数は、動的な特性を持つ素子としてインダクタとコンデンサの2つが存在するので、2次遅れ要素を含むものになりました。電流不連続モードの場合、インダクタに蓄えられるエネルギーはスイッチングの毎周期でゼロとなるため低周波領域では動的な特性を持たず、コンデンサのみが動的な素子となるため、1次遅れの伝達関数となります。また、電流連続モードでの昇圧コンバータや昇降圧コンバータが持つ不安定零点も、電流不連続モードでは有しないため、制御系の設計が簡単になるということになります。

まとめ

昇圧コンバータを主な例とし、状態平均化法による解析とモデル化の過程を解説していきました。単純な回路構成のスイッチングコンバータではありますが、その詳細な解析手法は複雑で理解するのが難しいものかと思います。伝達関数モデルやその導出過程を知っておくことで、実際にスイッチングコンバータの制御系の設計や考察をするときに役に立つでしょう。

タマゴさん

電子工作初心者のパワエレ幼女です。マジでド素人なので記事内容はあまり参考にしないほうがいいかもしれません。