幼女でもわかる 三相VVVFインバータの製作
おはようございましたタマゴさんです。
テスラコイルを作ることに集中してたら、いつの間にか今年度がほとんど終了しており、もう一度同じ学年に居座ることになりました。
結構ワロエナイ状況です。高専とはこういうところですので、趣味は程々に、課題だけは必ず提出しましょう。
さて、テスラコイルやスイッチング電源をはじめとして、パワーエレクトロニクスを勉強して遊んでいる今日この頃ですが、今回は、単相交流電力(商用電源AC100V)を三相交流電力に変換する、AC-ACインバータを製作してみることにしました。
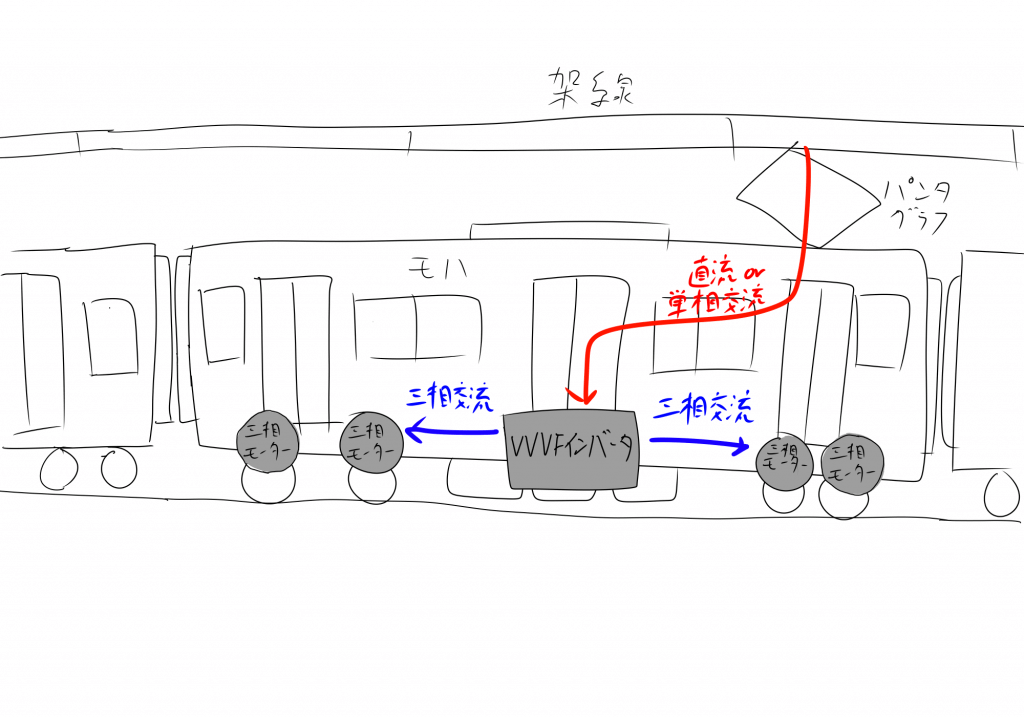
インバータは、電車に使われているような、三相モーターを回転させるために使用されているのが有名です。電車は、架線とレールを通る、直流又は単相交流を電源としています。また、電車の車輪を回転させるために、主に三相誘導モーターが使われています。
これらのことから、架線から得た直流又は単相交流を、モーターを回転させるための三相交流に変換する、インバータが必要となるわけです。
三相誘導モーターは、周波数と電圧を可変させることのできる三相交流を使うことで、回転速度やトルクを自由に制御することができます。周波数と電圧を可変できる三相交流を得られるインバータは、VVVF(Variable Voltage Variable Frequency、可変電圧可変周波数)インバータと呼ばれています。
実際に三相誘導モーターを制御してみるため、VVVFインバータを製作することにしました。
いやぁすごく基本的なことから書いてしまったのでさすがにそれくらいはわかるよ~っていう方はすっとばしながら読んでください。。。
1. 基礎知識編
1-1. インバータのしくみ
では、具体的にどのようにして交流電力を発生させる回路が作れるか見ていきましょう。
まず、簡単な単相インバータを考えてみます。
単相交流は、時間が経過するごとに、正弦波状に電圧が上下を繰り返しています。つまり、正弦波の電圧を発生させることができる発振回路があれば、単相交流を生成することができるわけです。
以下に、正弦波発振回路の例を示します。
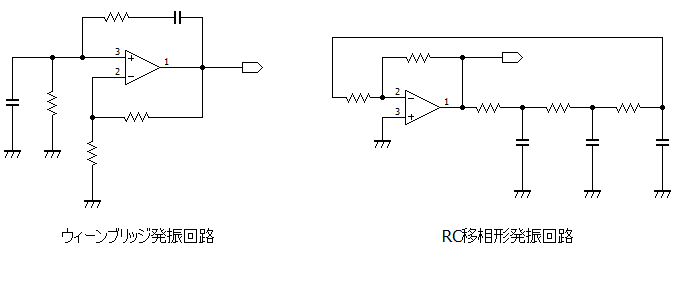
確かにこのような回路があれば、単相交流を得ることができます。しかし、実際に必要になる交流電源は、大電力を必要とする交流モータの場合、高電圧、大電流の出力が必要になります。
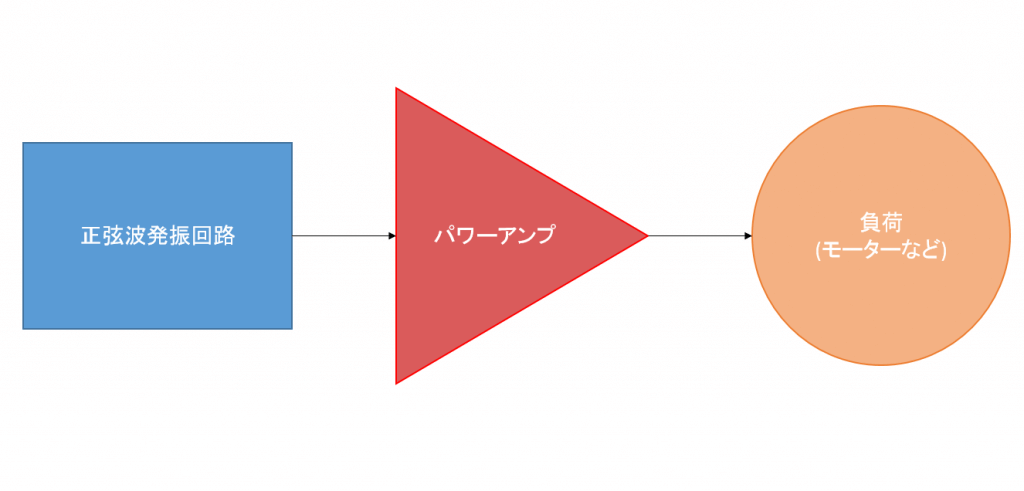
発振回路単体では、直接高い電力を得ることはできません。(できなくはなさそうだが、非常に大きく高価な部品がたくさん必要となり、効率も良くない)
したがって、発振回路で得た正弦波を、パワーアンプで電力を増幅させれば良いわけです。
1-2. D級アンプとPWM
パワーアンプはさまざまな回路の方式があり、必要な出力、効率などから最適なものを選択します。
有名なアンプ回路の一例として、A級トランス結合型、AB級プッシュプル型は、A級RC結合型に比べて効率が高く、大きな出力を得ることができます。
しかし、これらの方式でも、数百W、数kWほどの出力を得ようとなると、それ相応にトランジスタによる損失が増え、大きな電力消費に耐えうる素子が必要となります。
そこで、さらに損失を少なくし、高効率化されたのがD級アンプです。
D級アンプのDとは、ディジタル(Digital)の頭文字を示すと言われており、A級、B級などのバイアスの掛け方を示す記号とは異なります。すなわち、それらとは全く異なった電力増幅方式です。
ディジタルとはONとOFFの2種類の状態しか存在しません。では、これでどのようにアナログの出力を得るのでしょうか。
例えば、LEDを段々と高速に点滅させていくと、いずれ人の目には点滅しているとは認識しなくなり、普通より暗く常に点灯しているように見えるようになります。
また、ONをする時間とOFFにする時間の割合を変化させると、明るさが変化しているように見えます。

このように、高速にONとOFFを繰り返し、ONする時間とOFFする時間の割合を変化させることで、擬似的にアナログが表現できるのです。
ON、OFFする周期が一定のまま、ONする時間とOFFする時間の割合を変化させて擬似的なアナログ信号を得る制御法を、PWM(Pulse Width Modulation、パルス幅変調)といい、ONする時間とOFFする時間の割合のことをデューティー(Duty)比といいます。
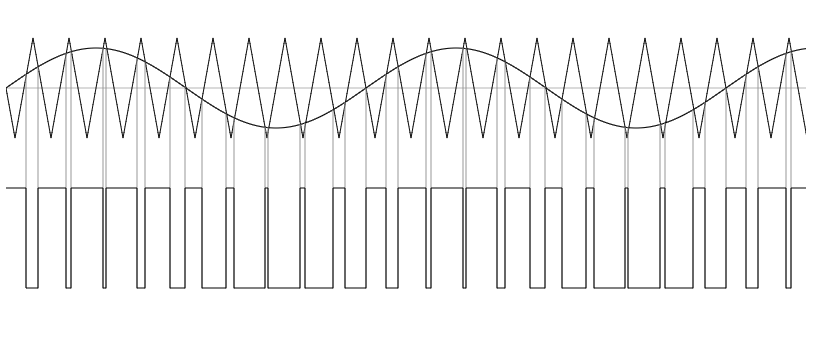
そして、正弦波に対してPWMを使うと次の図ような波形になります。
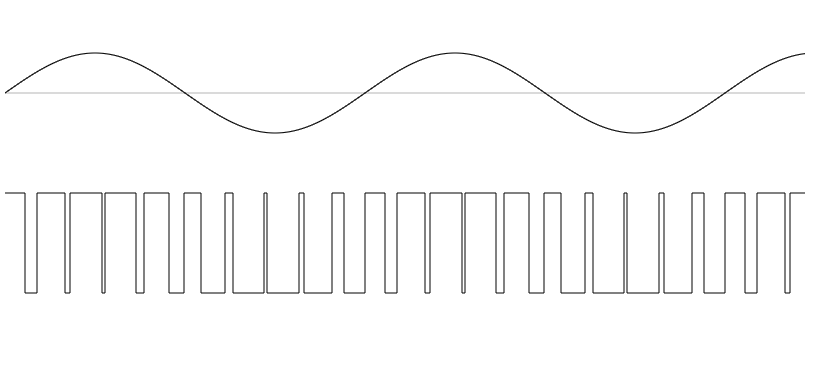
PWM信号の作り方として、このように三角波と比較して、三角波よりも高い場合はON、低い場合はOFFとしたときの矩形波を得る方法があります。
この図に示す正弦波を変調波、三角波を搬送波といいます。
スイッチ2つを上下に置いた次のような回路があります。このスイッチのペアでハーフブリッジ回路と呼ばれます。
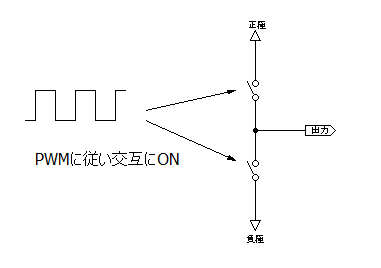
これにPWMを使い、それぞれのスイッチを交互にON、OFFすることで、スイッチの中間点から、電力的に増幅された変調波が出力されます。これがD級アンプの原理です。
このスイッチには、FETやIGBTが使われ、ONかOFFかのはっきりした駆動がされるため、素子による電力消費がほとんどなくなります。そのため、D級アンプは、非常に高い効率が実現でき、大電力の出力が可能となるアンプなのです。よって、インバータにはD級アンプが用いられます。
1-3. インバータのブリッジ回路
単相交流とは2本の線に180°ずつ位相がずれた電流、そして、三相交流とは3本の線に120°ずつ位相がずれた電流です。
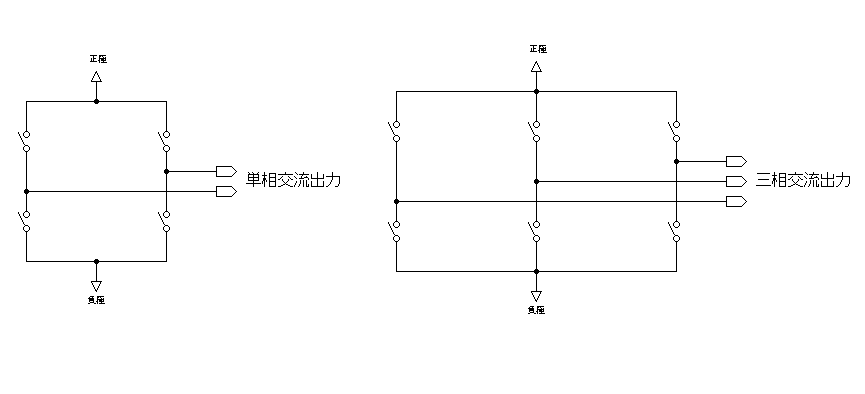
単相交流を出力するインバータは、ハーフブリッジを2つ並べます。この形の回路はHブリッジやフルブリッジと呼ばれます。
そして、それぞれのハーフブリッジに2本の相、つまり180°ずれた(反転した)正弦波のPWMを使い、駆動すると、単相交流が得られます。
三相交流の場合は、ハーフブリッジを3つならべ、同様にして、120°ずつずれた正弦波のPWMをそれぞれに使うと、三相交流を得られます。
つまり、単相インバータの場合、スイッチの素子は4つ、三相インバータの場合は6つ必要になります。
2. 考察編
2-1. 三相正弦波発振回路
三相インバータに必要な変調波である、120°ずつ位相がずれた正弦波を得ることができる発振回路を考えてみましょう。
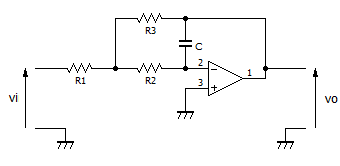
ます、有名な正弦波発振回路の一つである、RC移相形発振回路を以下に示します。
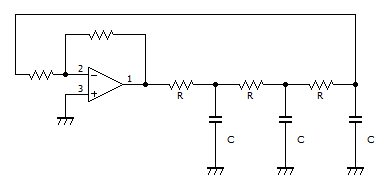
コンデンサCと抵抗Rによる積分回路が3段重ねになっており、反転増幅させてループさせるような回路です。
RC回路では、入力と出力の位相差を0°から90°未満までずらすことができます。
発振回路が安定して発振する条件は、ループ状の回路全体の利得が1であること、そして、ループしたときの位相が一致していることです。
このRC移相形発振回路の原理は、RC回路3段で180°位相をずらし、さらに反転させることで、ループした時の位相が360°ずれる、すなわち一周回って位相が合うようになることによって発振します。
RC回路3段で180°ということは、1段でちょうど60°ずれるような周波数で発振します。
つまり、1段目と3段目の出力、2段目を反転させた出力を得ることによって、それぞれ位相が120°ずつずれた、三相の正弦波を得ることが可能となります。
この発振回路を解析してみましょう。発振回路の等価回路を考えると次のようになります。
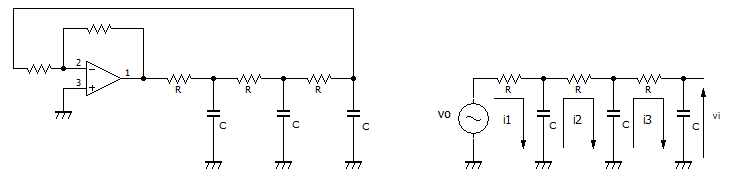
まず、コンデンサCのリアクタンスを
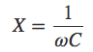 とし、オペアンプの入力インピーダンスは無限大と考えると、
とし、オペアンプの入力インピーダンスは無限大と考えると、
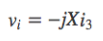 となります。
となります。
RC回路それぞれに、ループ電流に関する方程式を立てると次のようになります。
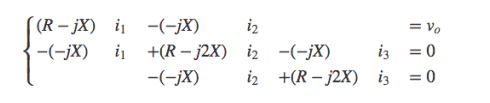
について解くため、行列式
を次のようにして表し、Cramerの公式を適用すると、
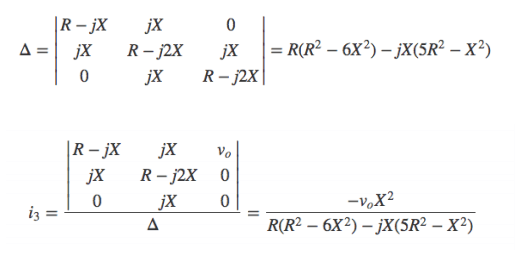
となるので、オペアンプに入力されるは、
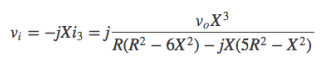 となります。よって、発振回路が安定して発振するためのオペアンプの増幅度は、
となります。よって、発振回路が安定して発振するためのオペアンプの増幅度は、
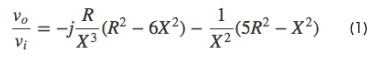 となりますが、オペアンプによる位相のずれは虚数ベクトル成分には発生しないので、虚部が0となります。
となりますが、オペアンプによる位相のずれは虚数ベクトル成分には発生しないので、虚部が0となります。
したがって、
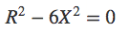 より
より
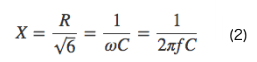 よって、発振周波数は
よって、発振周波数は
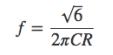 となります。
となります。
また、式を
に代入すると、
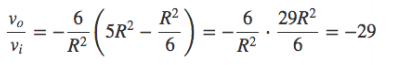 となるので、増幅度を-29にすることで、安定して発振するようになります。
となるので、増幅度を-29にすることで、安定して発振するようになります。
実際にシミュレーションしてみた結果がこちらです。
RC回路それぞれのノードから60°ずつずれた正弦波が出ているのがわかります。これに三相正弦波を取り出すような回路を追加すると、
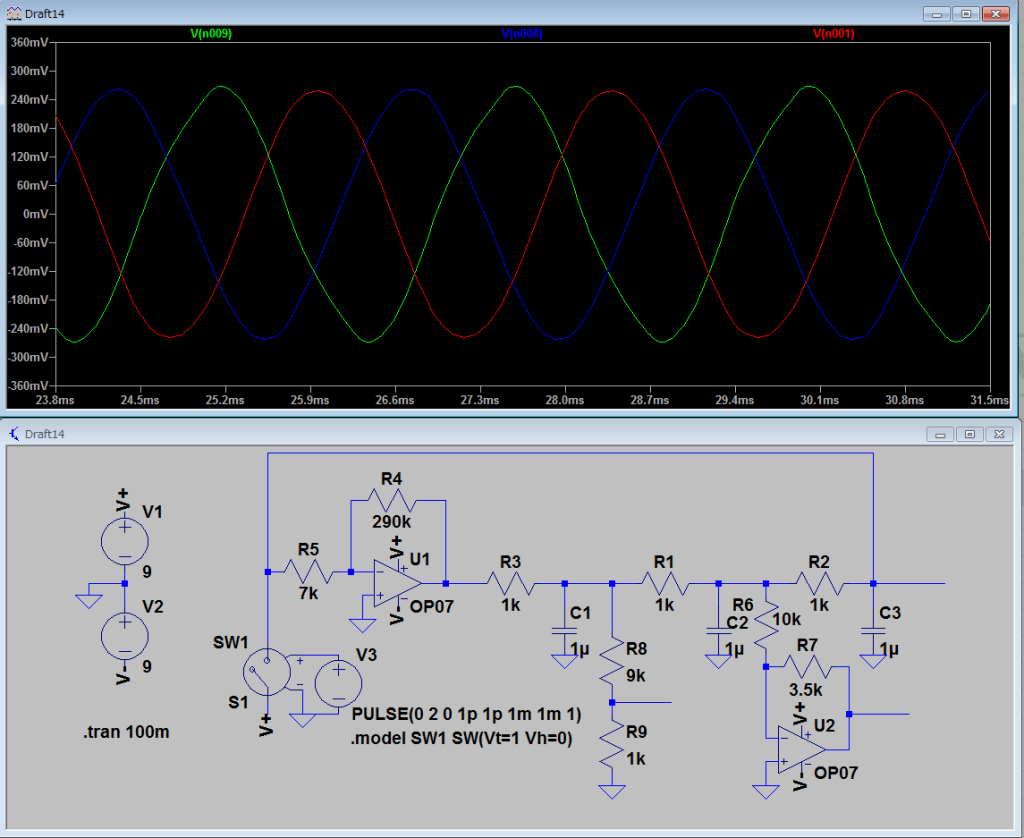
こうなります。最大電圧が最も小さくなるRC回路3段目の電圧と同じ電圧になるように利得を調整しました。
しかし、Rの値を変え、周波数を変えてみると、
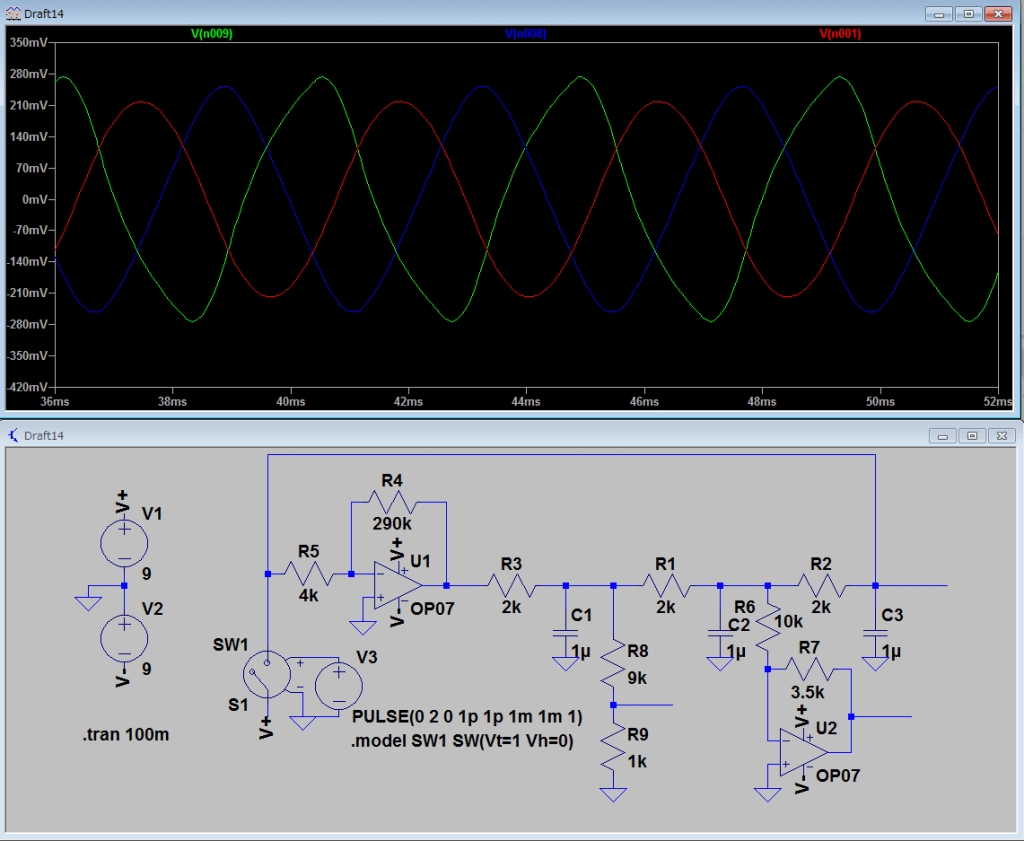
大きさがずれるどころではなく、波形が歪んでしまうのがわかります。
オペアンプの出力部分を見てみると
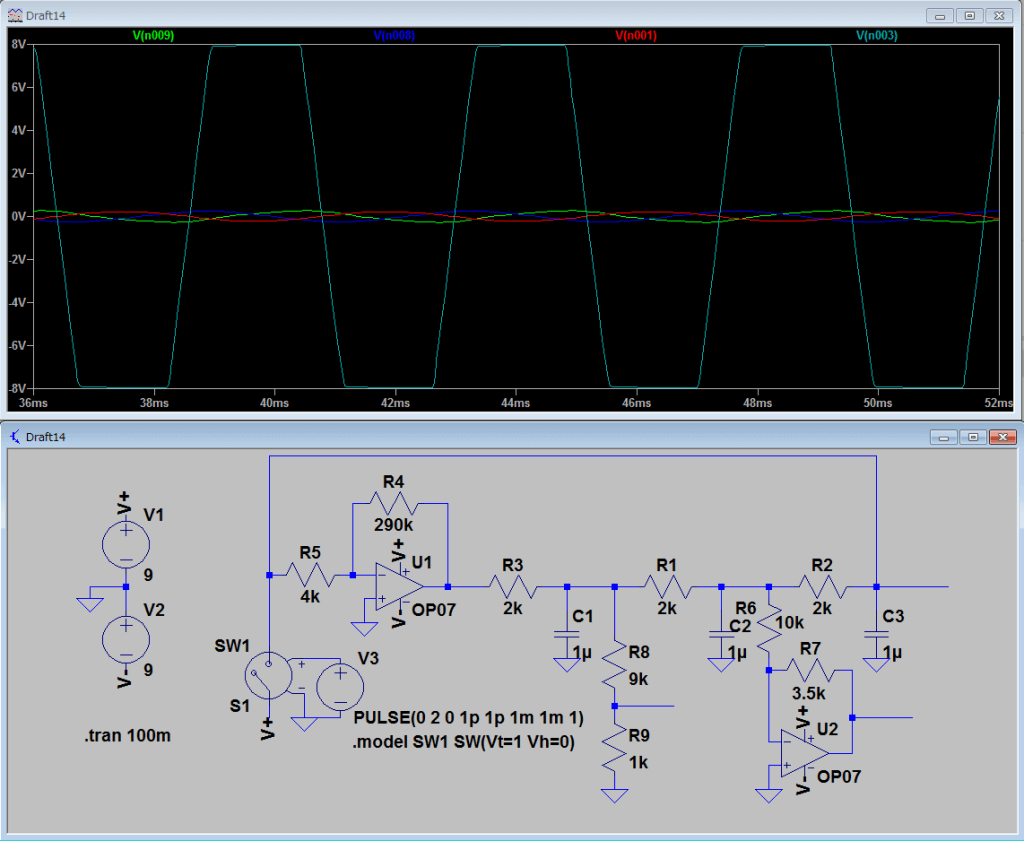
短形波に近い形になっています。これは、増幅度が大きすぎて出力の限界に頭打ちになっている、すなわち飽和してしまっているということです。
発振周波数を下げるために、Rの値を大きくしていくと、RC回路における利得の減衰が大きくなり、その分オペアンプで大きく増幅しなければなりません。
しかし、そうすると飽和が起こり、結果的に波形が乱れてしまうことになるのです。
つまり、VVVFインバータとして必要十分なほどの帯域で周波数を変化させるのは、この回路では難しいということになります。
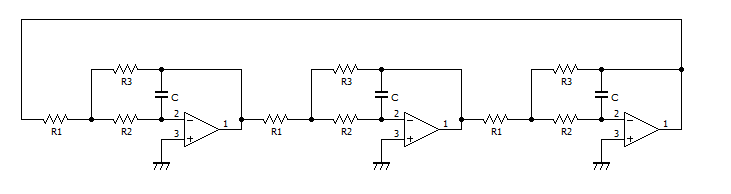
RC移相形発振回路での問題であった、RC回路での利得の減衰を改善した回路がこちらです。
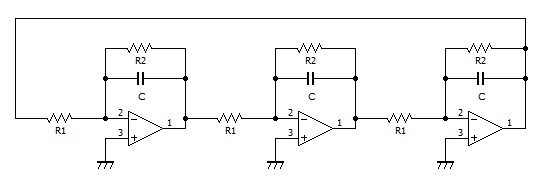
RC積分回路にオペアンプを用いたものを3段重ね、ループさせたものです。
この積分回路1段は反転を含むので、180°~270°の位相を遅らせることができます。
つまり、1段で240°、3段で720°ずらすような発振回路となっており、三相正弦波を得ることが可能となります。
この積分回路の伝達関数は、次のようになります。
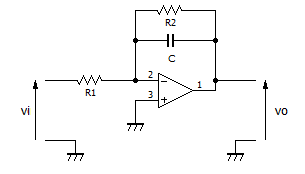
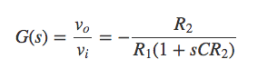
とし、これが3段重なったときのループ利得は、
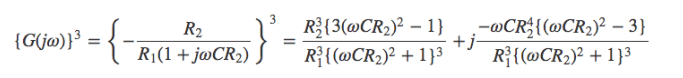 となり、発振するための条件を実部と虚部に与えると、次のようになります。
となり、発振するための条件を実部と虚部に与えると、次のようになります。
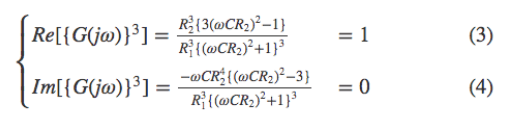 式
式より、
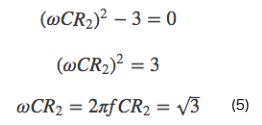 よって、発振周波数は、
よって、発振周波数は、
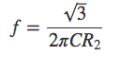 となります。
となります。
また、式を式
に代入して、
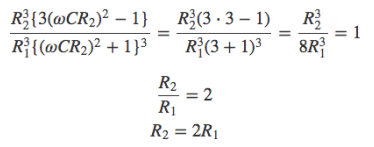 となり、これが安定して発振する条件になります。
となり、これが安定して発振する条件になります。
ちなみに、のときは、ループ利得は1より大きくなり、
のときは、1より小さくなります。
実際にシミュレーションしてみます。
のとき
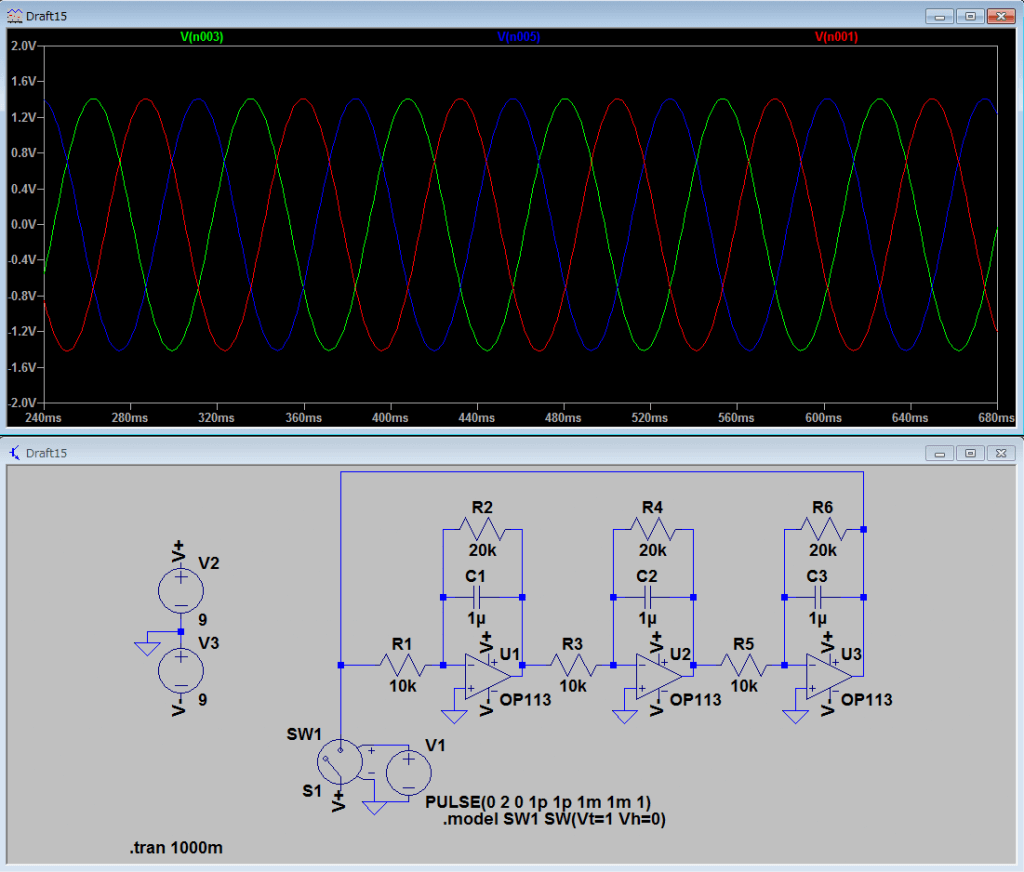
安定して発振し続けているのがわかります。
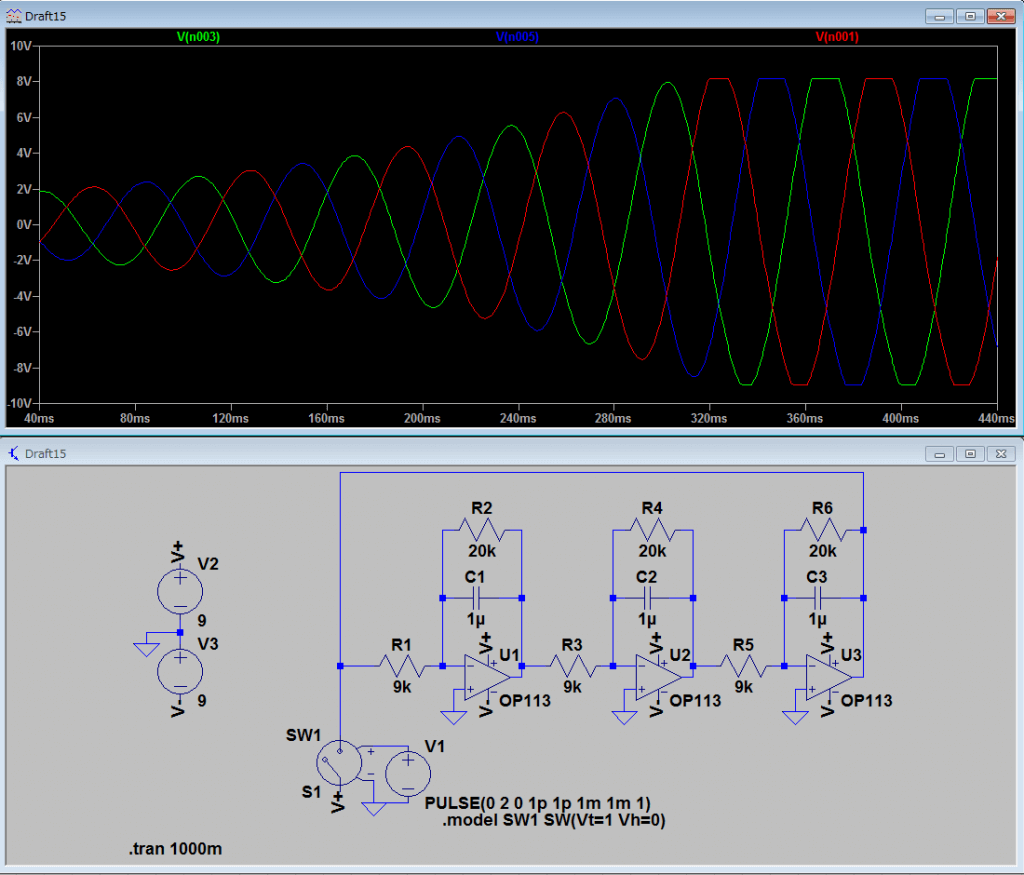
徐々に振れ幅が大きくなっていき、飽和してしまいます。
徐々に振れ幅が小さくなっていき、消えてしまいます。
つまり、安定して発振したまま周波数を可変させるためにはと
を同時に変化させる必要があるのです。
実際に回路を制御するためには、定数を変化させる素子は最小限に抑えたいところです。
そこで、その問題をさらに改善した回路がこちらです。
原理は先ほどとほどんど変わりなく、少し変則的な積分回路のようなものです。
この回路1段分の伝達関数は次のようになります。
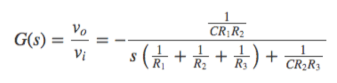
とし、これが3段重なったときのループ利得は、
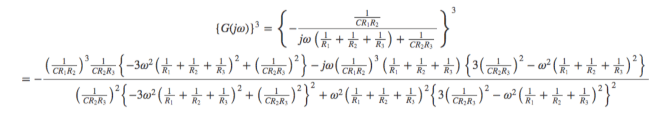 となります。ここで
となります。ここで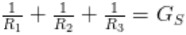 とし、
とし、の実部と虚部に発振するための条件を与えると、次のようになります。
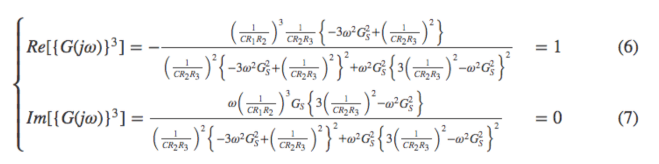 式
式より、
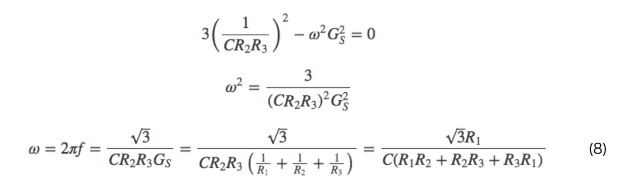 よって、発振周波数は
よって、発振周波数は
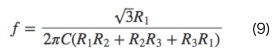 となります。
となります。
また、式より、
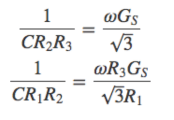 となり、これらを式
となり、これらを式に代入すると
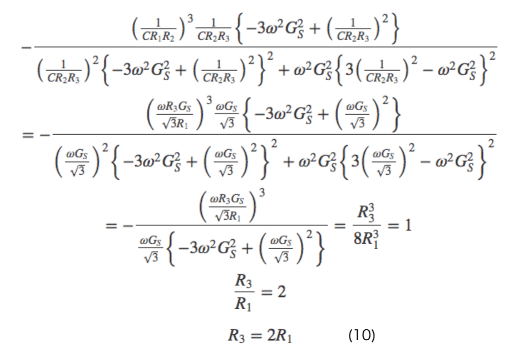 となり、これが安定して発振する条件になります。先ほどの発振回路と同じようになるのがわかります。
となり、これが安定して発振する条件になります。先ほどの発振回路と同じようになるのがわかります。
式を式
に代入すると、
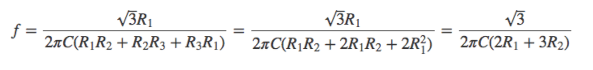 となります。つまり、
となります。つまり、だけを変化させることにより、式
の条件を保ったまま、周波数を可変できるということです。
シミュレーションしてみると、
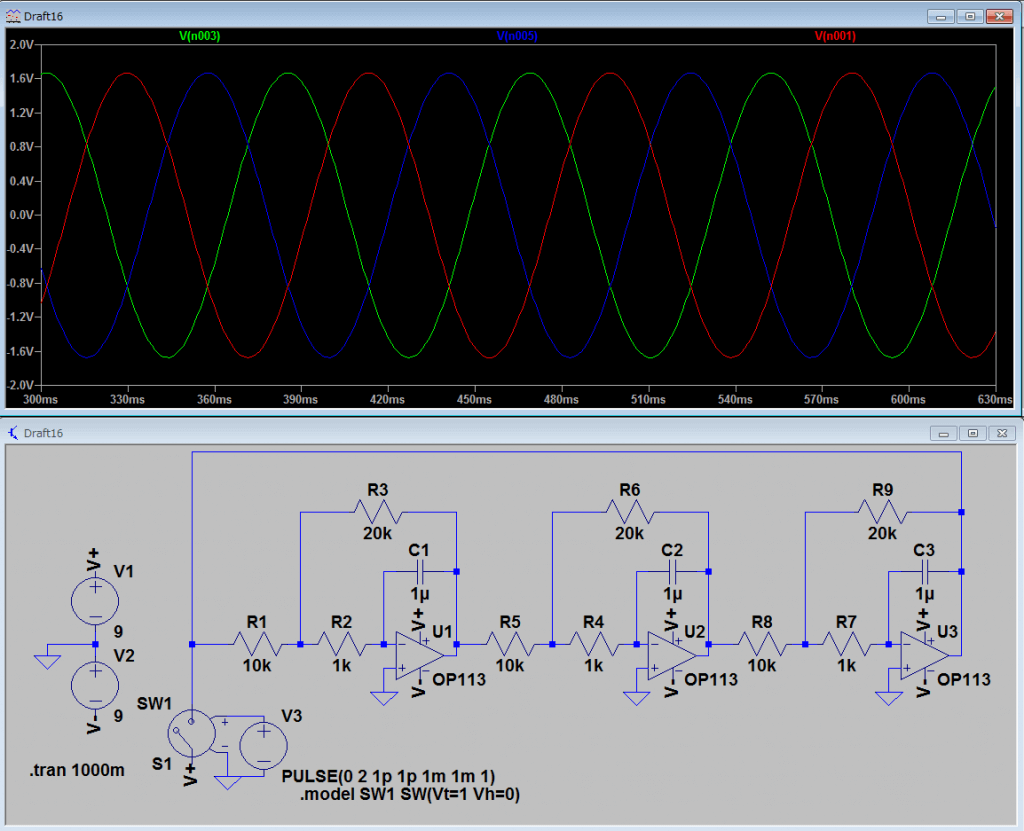
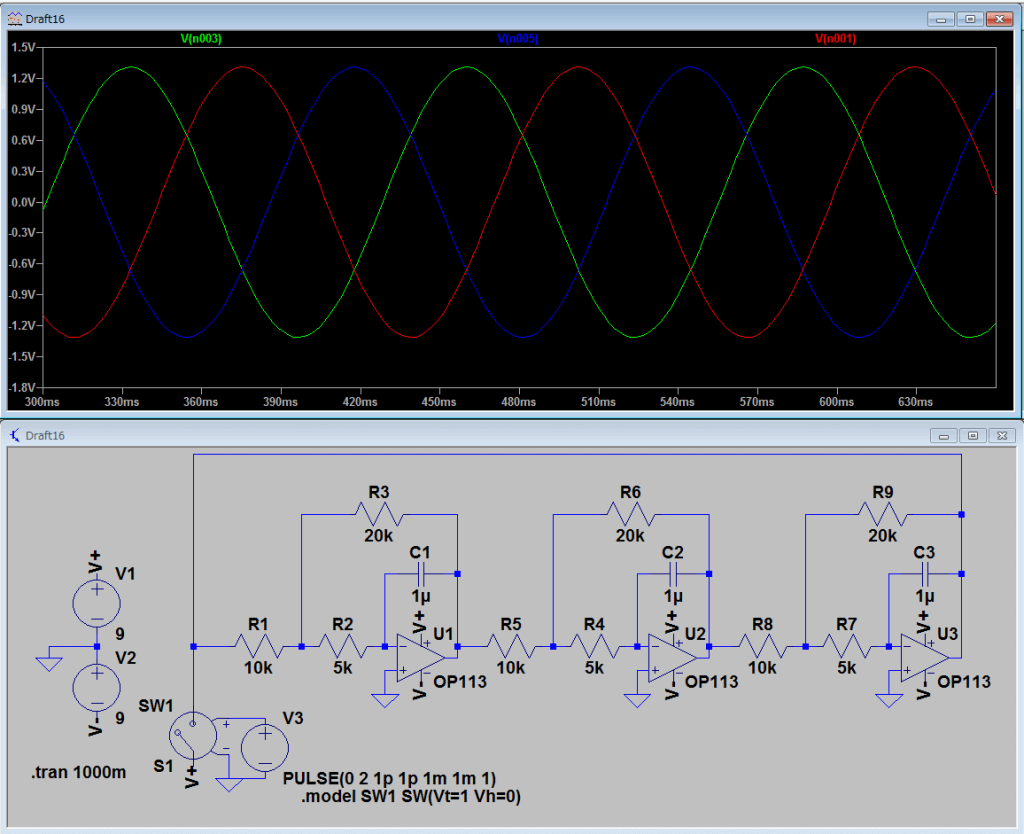
このように、に該当する抵抗だけを変化させても、安定して発振し続け、発振周波数を可変できることがわかります。
よって、この発振回路を製作に使うことにします。
2-2. 三角波発振回路
PWMの搬送波である、三角波を得るための発振回路も必要です。
三角波発振回路を以下に示します。
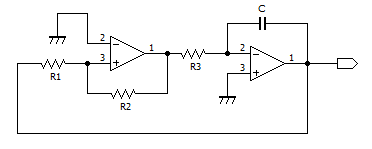
ヒステリシスコンパレータと積分回路がループ状に組まれた回路です。
動作原理は簡単ですので説明を省きます。
発振周波数と出力電圧最大値を以下に示します。
 なお、発振条件は
なお、発振条件はです。
3. 設計編
設計したVVVFインバータの回路はこちらです。
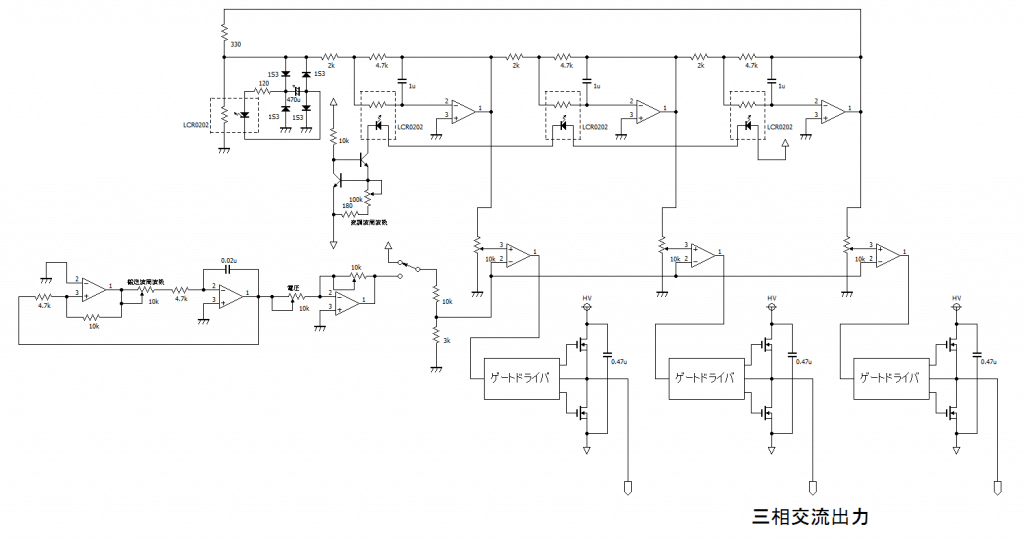
正弦波と三角波をコンパレータに通してPWM信号に変換し、ゲートドライバに入力されブリッジ回路が駆動されるという仕組みです。
三相正弦波発振回路部分です。
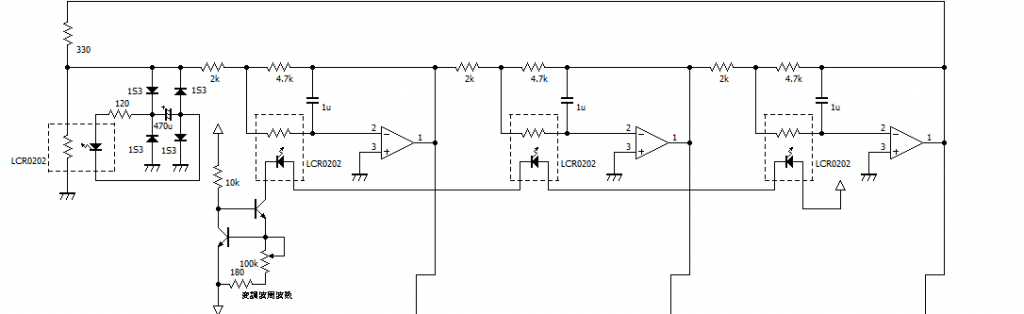
周波数調整にアナログフォトカプラを用いて、入力する電流の大きさに応じて周波数を変えられるようにしました。
これがアナログフォトカプラのLEDの電流を調整するための定電流回路です。
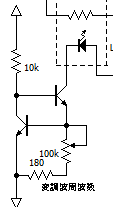
可変抵抗で、流す電流の大きさを制御でき、発振回路の周波数が可変できます。
また、わざと発振回路1段分の利得が1より大きくなるように抵抗値を設定して、自動的に利得を下げループ利得を安定化させる回路を入れることにより、実際の回路でも自動的に起動し、安定して発振するようにしました。
電圧の調整は、変調波(正弦波)の大きさを固定し、搬送波(三角波)の大きさを変えることとしました。
三角波を出力をした先に、利得を調整するオペアンプをつけます。このオペアンプの入力抵抗を0にすると増幅度が無限大となり、正弦波と比較した時、PWM信号として現れる電圧は0となります。
実際に製作する回路はこちらです。
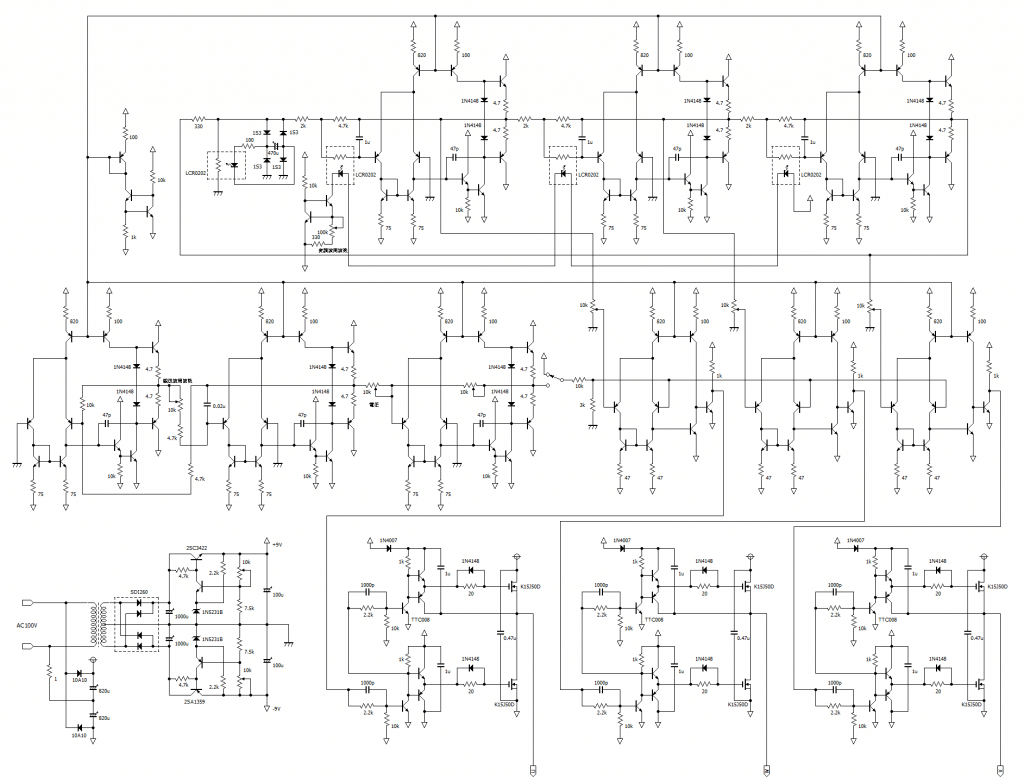
オペアンプやコンパレータの内部回路はトランジスタで構成し、電源回路やゲートドライバにはICを使わず、シンプルな回路にしました。
ゲートドライバとブリッジ回路部分を以下に示します。
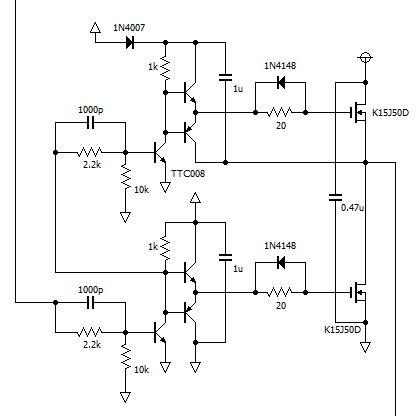
プッシュプル回路を使い、ゲートを低インピーダンスで駆動させます。
ブートストラップ回路を用いてハイサイド側のFETも駆動できます。ハイサイド側のプッシュプルを駆動するのトランジスタは、ブリッジ回路の電源電圧以上の高耐圧なものを使用します。
電源回路部分です。
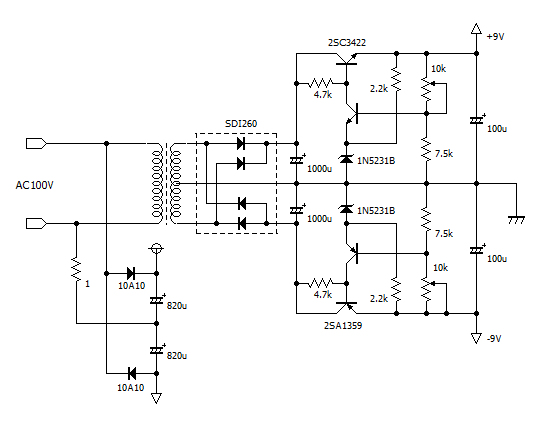
手元にあった適当なトランス(100V→-15V 0V 15V)を使い、正負電源を出力するリニアレギュレータを構成しました。
電圧降下をさせるためのトランジスタは、コレクタ損失の定格が大きめのものを使います。
また、倍電圧整流回路を使いDC280Vに昇圧して、ブリッジ回路の電源としました。
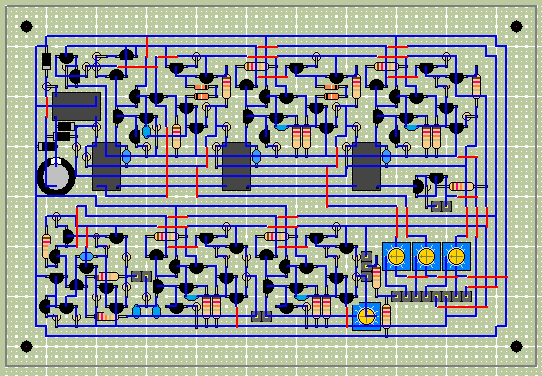
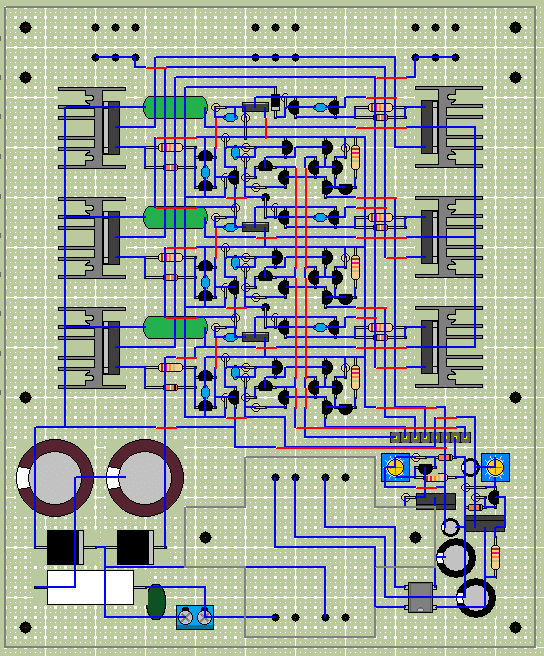
ユニバーサル基板の配線パターン図を以下に示します。
三相正弦波発振回路と三角波発振回路部分です。
電源回路、コンパレータ、ゲートドライバ、ブリッジ回路部分です。
4. 製作編
基板に実装していきます。


発振回路部の基板が出来上がりました。


動作確認です。


三相正弦波、三角波、どちらも正常に発振しています。
もう一方の基板も作っていきます。

バイポーラトランジスタは全部で111個です。

電源回路、ブリッジ駆動回路部の基板も出来上がりました。


動作確認です。FETのゲート電圧の波形を確認します。
正弦波がPWM信号となって現れているのがわかります。
コントローラのようなものも作ります。

組み立て、三相誘導モーターを接続します。


電源を入れ、電圧、変調波周波数をあげていくと、モーターが回転し始めました。

動作している様子です。
ピーと聞こえる音は搬送波の音です。搬送波の周波数を変えると聞こえる音の高さが変わります。
5. まとめ
実際に三相VVVFインバータを作り、三相誘導モーターの回転を制御することができました。
今回製作したものは、搬送波と変調波それぞれの周波数が関係していない、非同期モードのみですが、一般的なVVVFインバータには、搬送波と変調波がある一定の周波数の割合で同時に変化させ、1周期分のPWMのパルス数が一定となる、同期モードが実装されます。これを実装するためには、さらに複雑な制御ができる回路が必要となり、マイコン等が使われる場合がほとんどのようです。
とにかく誘導モーターを回してみたいという方は、非同期モードのみのインバータを作ってみてはいかがでしょうか。

参考文献
藤巻忠雄 大庭勝實 本多貴史 (1996)『電圧制御三相正弦波発振器』J-STAGE
https://www.jstage.jst.go.jp/article/ieejeiss1987/116/12/116_12_1420/_pdf
須田健二 土田英一 (2003-2016)『電子回路』コロナ社
電子工作初心者のパワエレ幼女です。マジでド素人なので記事内容はあまり参考にしないほうがいいかもしれません。



全てディスクリートで作る、凄いです。
これなら留年しなくてもいいのじゃないの
vvvfで音楽を奏でてるのはどのようにしてるでしょうか?
PWMの周波数(搬送波の周波数)を音階にしています
トランスはこちらを使っても大丈夫ですか?
http://akizukidenshi.com/catalog/g/gP-08734/
記事にはー15v、0v、15vを使ってることになっていますが、-15vが出力されるトランスは探しても見つかりませんでした。
それでも使えると思いますがこちらのほうがおすすめです。
http://akizukidenshi.com/catalog/g/gP-08732/
製作は自己責任でお願いします。
返信ありがとうございます。
当然のことですが、自己責任で制作します。大変助けになりました。
回路図にありました、三相交流発振回路に接続されている4つのダイオード、アナログフォトカプラ、コンデンサで構成されている(利得を安定させる?)回路の詳細について教えて頂いてもよろしいでしょうか?
大まかな動作原理は、発振の振れ幅が大きくなると大きく減衰させ、振れ幅が小さくなると小さく減衰させるという動作の繰り返しで利得を一定に保っているという仕組みです。
ダイオードブリッジとコンデンサで発振信号を整流、平滑してアナログフォトカプラのLEDに入力しています。振れ幅が大きくなると、アナログフォトカプラのLEDに電流が多く流れ、CdS側の抵抗値が小さくなり、330Ωの抵抗との分圧による減衰が大きくなります。また、振れ幅が小さくなると、LEDに流れる電流は小さくなり、CdSの抵抗が大きくなり、330Ωの抵抗との分圧による減衰が小さくなります。
なるほど。高度なフィードバック回路だったんですね。
解説ありがとうございます。
失礼します。
回路図にある型番が書かれていないトランジスタはどれを使われたんでしょうか?
2SC2120と2SA950を使用しました。2SC1815と2SA1015などでも大丈夫だと思います。
音色を変えるにはどうするんですか?
音色というのは、音階のことでしょうか?
音階は搬送波の周波数を変えれば変わりますよ。
低ワットの電子スライダーを(デューティ制御でなく)作ってほしいぞ。
VVVFで周波数50Hz、60Hz固定で
EG8010が利用できるともっといいな。
商品化できるんじゃないでしょうか?
このサイト内の回路図等画像を使わせていただきたいのですが、どの程度までならよろしいのでしょうか?
写真とイラスト以外の画像(回路図、配線図、シミュレーション画像など)なら使用して頂いても構いません。ただし商用利用はご遠慮ください。
早急な返信ありがとうございます。
規約に従って使わせていただきます。
プッシュプルとブートストラップを用いたハーフブリッジの部分、デッドタイムはどの様にして設けているのですか?同一回路をブレッドボードで組み、矩形波を投入しても貫通電流は観測できなかったのですが、謎が深まります。
ゲート抵抗に対して並列にダイオードを設けることで、ターンオフ時のゲート電荷を速く抜き、ターンオン時間よりもターンオフ時間を短くすることで簡易的に貫通電流を抑制しています。
幼女には理解できても、私にはとても(TT)
三相正弦波発振回路の主電源はどのようなものを使っているのでしょうか?
こんにちは。初めまして。
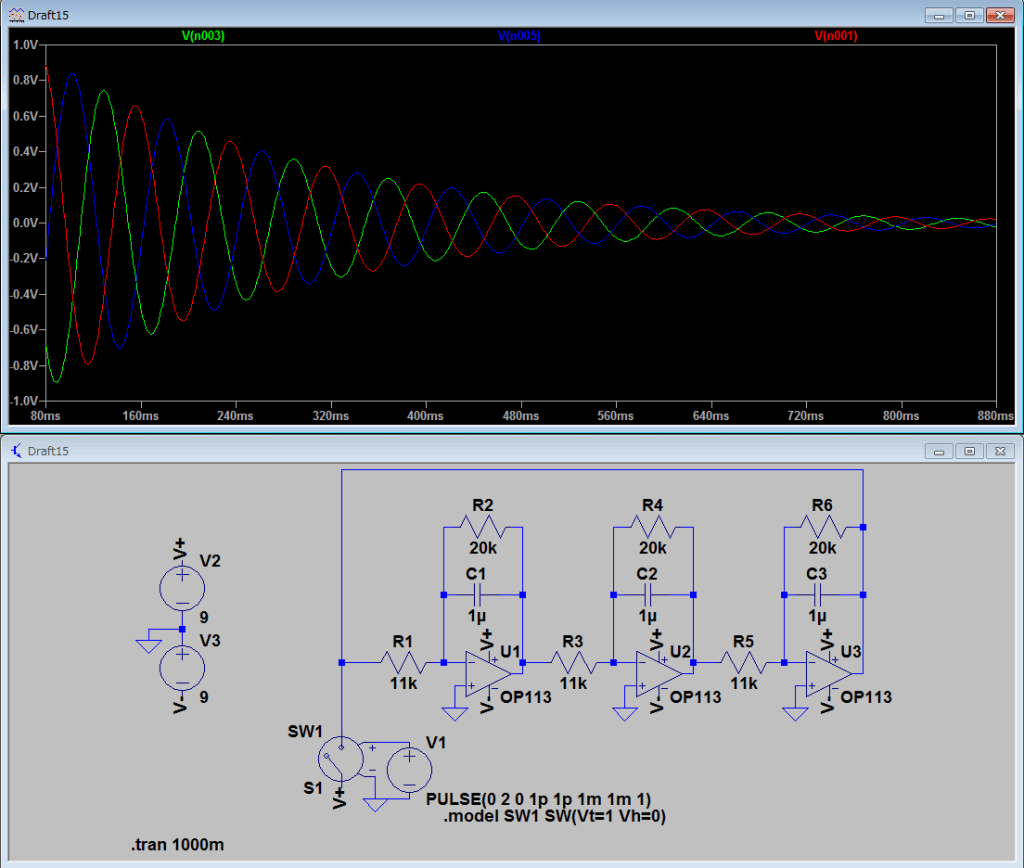
質問がありまして、シミュレーションにて三相発振回路の電源をPULSEとSWを使ってる理由は何でしょうか?
参考にさせて頂いているのですが、知識不足で理解できなくて。
あと、お手数でなければシミュレーションの電源の設定の下にある.modelの設定はどのようにするのか、ご教示頂ければ助かります。
どうぞ、よろしくお願い致します。
理由は、初期条件にあたる電圧がないと当然のごとく回路はウンともスンとも言わないからです。PE初心者さんも定量的な考察を理解したいことと存じます。そのためには、本来、定常状態正弦波にしか使えないインピーダンス計算を発振回路の考察に使ってしまっているタマゴさんのばかな記述は不要で、定数係数微分方程式を出力電圧(3つ)について立て、それを演算子法の定理を使って解く必要があります。すると、正弦波の振幅は、初期電圧(2V)の2/3倍(1.3V)であることが計算され、数値的なシミュレーション結果を解析的に厳密に理解することが可能となります。
理想的な発振回路は定常的に正弦波となるため,微分演算をs=jωとして定常特性を解析することができます.過渡的な動作を解析するには時間領域での計算が必要ですが,ここでは発振周波数を求めるため定常特性しか記述しておりません.
仰ってる2Vという電圧はSWを駆動しているだけのパルスのことかと思いますが,発振回路そのものとは全く関係ない電圧です.
YouTubeでもお世話になりました。私は、元(大学)生徒で、去年から無能な公務員をやらせていただいております。タマゴさんのような偉大な技術者を目指して、第二種電気工事士を取ったり勉強を重ねてきました。弛張発振回路(マルチバイブレータ)という、単一正弦波を発振することのない発振回路があることを忘れてしまうくらいタマゴさんを困惑させてしまいすみませんでした(もちろん、まだ私は、マルチバイブレータを理解していません)。複雑なものづくりをできることはすごい上に憧れますが、コイルのインピーダンスがjωLでコンデンサのインピーダンスが1/jωCである理由は、正弦波の複素数表示であることを理解できなかったのはお気の毒です。もちろん、理論でタマゴさんに追いついたと言う気はありません。制御工学がほんとに教科書の中だけの存在で、PID(K, 1/s, s)って結局なんだっただろうというレベルで、タマゴさんの最新記事を前にしてはフリーズしてしまいます
>>コイルのインピーダンスがjωLでコンデンサのインピーダンスが1/jωCである理由は、正弦波の複素数表示であることを理解できなかったのはお気の毒です。
そのように勝手に判断された訳はわかりませんが,この記事を書いた時点(5年前)でjωはラプラス変換された函数空間においてsinωtの振動を示すことは知っていました.
正弦波発振回路の話をしているのに,非安定マルチバイブレータのような非正弦波発振回路を急に挙げられているのも意味不明ですね.
マウントを取りたいのかは存じ上げませんが,第二種電気工事士などという誰でも簡単にとれる資格をステータスのように掲げたり,私の最新記事(幼女でも作れるというタイトルのように超基本的なこと)さえ理解できないのであれば,今更技術者を目指すのは無駄だと思いますので諦めることをお勧めします.
初めまして。
ヒートシンクのサイズを教えていただけるでしょうか。
基本的な質問でお手数をおかけし恐縮ですが、ご回答よろしくお願いいたします。
初めまして。
三相モーターはメーカーと型番をお教えしていただけるでしょうか。
ご教示頂ければ助かります。
どうぞ、よろしくお願い致します。